Human-level control through deep reinforcement learning

문제 정의

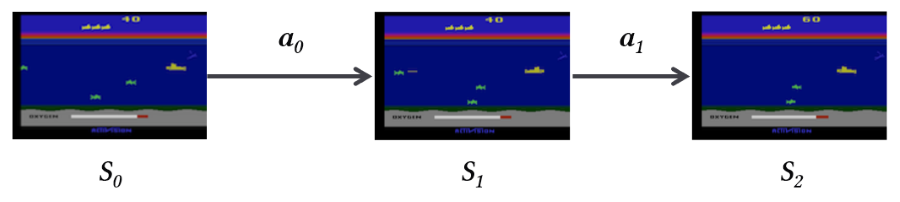
게임(Atari 2600)을 플레이하는 상황을 State, Action, Reward를 가진 MDP(Markov Decision Process) 상황으로 해석할 수 있다. 하지만 각 state가 복잡해서 state-action value를 정의하기 어렵다. 따라서 Convolutional Network을 사용해 state에서 특징을 추출하고, Feed Forward Network를 통해 state-action value를 예측한다.

• State: 게임 화면 (픽셀 이미지)
• Action: 게임기를 통해 각 time-step마다 입력된다.
• Reward: 게임 내 점수 변화

학습된 agent가 게임기를 통해 reward를 높이는 방향으로 행동하는 것이 최종 목표다. 참고로 본 알고리즘은 model-free & off-policy이며, behavior distribution은 $\epsilon$-greedy를 따른다.

Optimal action-value function 는 Bellman 방정식에 따라 $Q^*(s,a)$로 정의한다.

\[Q^*(s,a)=\mathbb{E}_{s'~\epsilon} [r+\gamma\max_{a'}Q^*(s',a')\mid s,a]\]

앞서 말했듯, $Q^*(s,a)$를 정확히 알 수 없기 때문에 neural network를 이용해 근삿값을 구한다.

\[Q(s,a;\theta) \approx Q^*(s,a)\]

딥러닝과 강화학습 비교

딥러닝에 비해 강화학습은 몇 가지 어려움이 있다.

• Correlated data
  • 딥러닝은 각 데이터 샘플이 독립적이지만, 강화학습은 일련의 과정을 학습하기 때문에 각 state 간 상관관계가 높다.
  • 딥러닝은 대량의 labeled data가 있지만, 강화학습은 환경으로부터 보상을 받으며 이마저도 불안정하고 지연된다.
• Non-stationary distribution
  • 딥러닝(지도학습)은 정해진 분포를 사용하는데 비해, 강화학습은 행동을 학습함에 따라 계속 변한다.

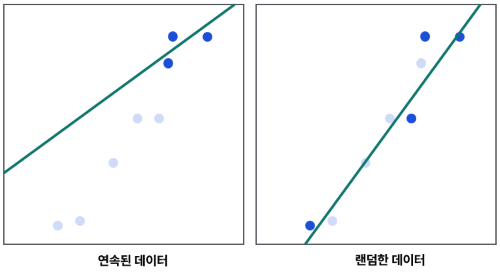
먼저 Correlated data란 상관관계가 높은 데이터를 뜻한다. 강화학습은 연속된 데이터를 받기 때문에 가까운 time-step의 정보는 비슷한 특성을 가질 확률이 높다.

예를 들어, Regression 문제를 푼다고 했을 때 가까운 데이터만 활용할 경우 편항이 발생한다. 반면 떨어진 정보를 이용하면 더 안정적으로 학습할 수 있다. 본 연구는 Non-stationary distribution을 이용해 문제를 해결했다.

두번째 문제는 목표가 변한다는 점이다. 딥러닝은 정해진 정답 레이블이 존재하고 변하지 않는다. 반면 강화학습은 학습과 동시에 target도 업데이트된다.

\[\textrm{Target}=R+\gamma\max_{a} Q(S',a)\] \[Q(S,A)\leftarrow Q(S,A)+\alpha [\textrm{Target}-Q(S,A)]\]

Q-learning에서 Target도 결국 Q-function을 사용하기 때문이다.

Non-stationary Target

다시 말해 목표가 계속 움직이다는 의미고, 불안정한 학습을 하게 된다. 문제를 해결하기 위해 행동을 결정하는 Q-network와 학습을 위한 Target network를 분리했다. Target network는 고정해 사용하다가 일정 시간이 지나서야 업데이트한다.

Q-function 학습

Value를 구하기 위해 파라미터 $\theta$를 이용한 neural network인 Q-network를 사용한다.

Q-network는 Loss function $L_i(\theta_i)$을 통해 학습한다.

\[L_i(\theta_i)=\mathbb{E}_{s,a}[(y_i-Q(s,a;\theta_i))^2]\]

$y_i$는 target으로 behavior distribution으로부터 샘플링한다.

\[y_i=\mathbb{E}[r+\gamma\max_{a'}Q(s',a';\theta_{i-1}^{-})\mid s,a]\]

파라미터 $\theta^-$를 이용한 neural network를 Target network라고 한다. 매번 업데이트되는 Q-network와 달리, 일정 iteration마다 업데이트된다. 일정 반복마다 Q-network 파라미터를 복사한다. 즉, Q-network와 Target network는 동일한 neural net이며 파라미터만 분리했을 뿐이다.

여담으로 Target network를 분리하지 않아도 Atari 게임을 잘 플레이하긴 했다. 본 기법은 2015 논문에서 소개되었고, 2013 논문에는 파라미터를 분리하지 않았다.

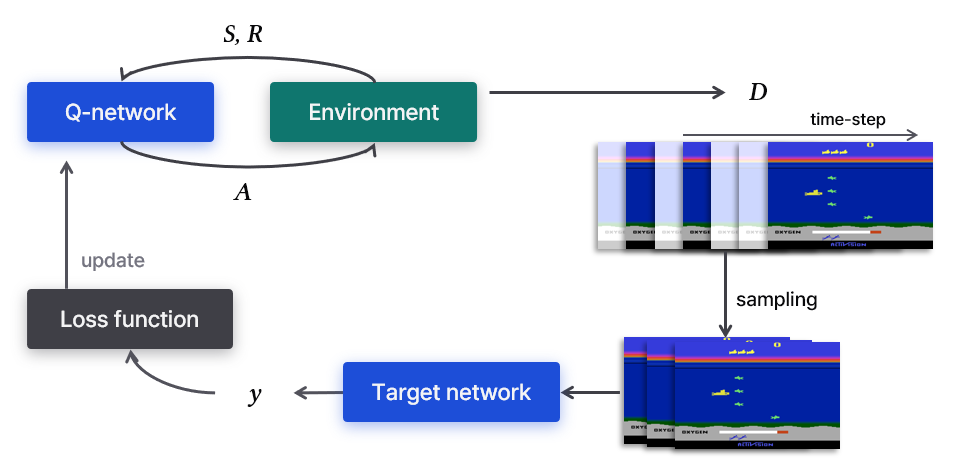
Experience replay

Experience replay는 agent의 경험 $e_t=(s_t,a_t,r_t,s_{t+1})$을 $D=e_1,…,e_N$에 저장한다. $y_i$를 구하기 위해 $D$로부터 랜덤하게 minibatch를 샘플링해 replay memory를 만든다.

이 방법은 여러 장점이 있다.

• 각 단계를 가중치 업데이트에 활용되기 때문에 효율적이다.
• 랜덤한 샘플을 사용해 데이터 간 상관관계를 줄였다.
• Behavior distribution이 여러 과거 state를 평균내어 계산하기 때문에 안정적으로 학습한다.
  • On-policy는 현재 파라미터를 기반으로 다음 행동을 결정하기 때문에 local minimum에 빠질 가능성이 있다.

전체 과정을 정리하면 다음과 같다.

위 코드는 2013 논문에 실린 코드로, Target network를 따로 분리하고 있지 않다. 하지만 본 글에서 소개한 알고리즘은 $y_j$를 계산하는 과정에서 $Q(\phi_{i+1},a’;\theta^{-})$를 사용한다는 차이가 있다.

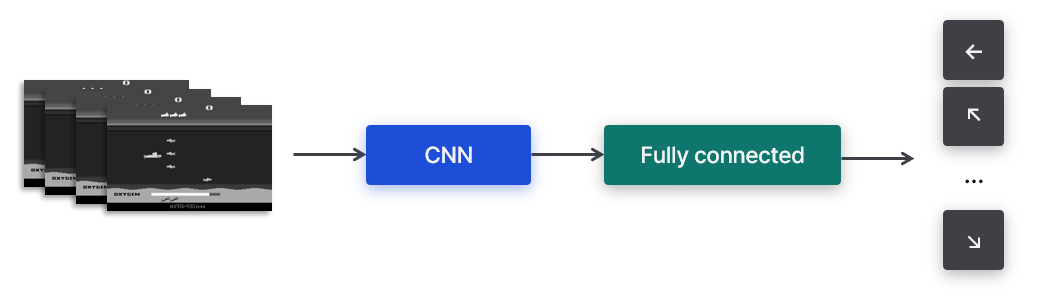
전처리와 모델 구조

• 게임 플레이 화면은 210x160 크기에 128개 색상을 가지는 RGB 이미지다.
• 110x84 크기, gray-scale 이미지로 변환한다.
• 게임 플레이가 진행 중인 부분을 중심으로 84x84로 자른다.
• CNN 네트워크에 입력한다.
• Fully-connected를 거쳐 다음 action을 출력한다.

결과

• Reward는 게임 내 점수에 따라 {-1, 0, 1}로 주었다.
• RMSProp에 minibatch 크기는 32를 사용했다.
• 학습 과정에서 behavior policy로 $\epsilon$-greedy를 사용했다.
• Frame-skipping을 사용했다.
  • 4n번째 프레임만 사용했다. (일부 게임 제외)
  • 스킵된 프레임에서는 이전 행동이 계속 유지된다.

기존 알고리즘에 비해 모든 게임에서 뛰어났다. 심지어 일부 게임에서는 사람보다 뛰어난 결과를 보였다. Q-network의 CNN을 t-SNE로 시각화한 결과, 비슷한 value를 가진 state끼리 가깝게 매핑된 것을 확인했다.

---

• Playing Atari with Deep Reinforcement Learning, 2013.
• Human-level control through deep reinforcement learning, 2015.