MDP에 대한 오해와 Value function 정의

강화학습을 처음 공부하면 헷갈리는 용어가 너무 많다. 특히 Markov Process를 잘못 이해하면 뒤에 나오는 모든 개념이 헷갈릴 수 있다. 본 글은 Markov Process에서 시작하는 여러 오해를 풀고, Value function이 어떻게 정의되었는지 살펴본다.

Planning과 Learning

강화학습 강의를 처음 들으면 Markov Process를 시작으로 Planning에 대해 배운다. 이 때문에 planning을 강화학습으로 오해하기 좋은데, planning은 강화학습이 아니다. 강화학습을 이해하기 위한 배경지식을 배우는 단계로 생각하면 된다.

Planning은 환경을 완전히 알고 있을 때 사용한다. 현재 상태에서 어떤 행동을 취할 수 있고, 행동에 따라 어떤 확률로, 어떤 상태로 진행되는지 모든 정보를 알고 있다. Planning은 Dynamic programming을 이용해 미래를 ‘예측’하는 것이지 ‘학습’하는 것이 아니다.

Learning은 환경의 일부만 볼 수 있다. Agent는 실제 행동하고, 결과를 관찰해 정보를 얻는다. Trial and Error를 반복하며 환경을 차근차근 알아간다. 실제 사람이 학습하는 과정과 비슷하다. Learning이 바로 강화학습에서 사용하는 ‘학습’ 방법이다.

Markov Decision Process

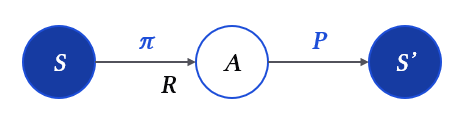
Markov Decision Process, 줄여서 MDP라고 부른다. MDP는 $<S, A, P, R, \gamma>$로 표현하며, 각 의미를 정확히 이해해야 한다.

• $S$: State. Agent의 현재 상태.
• $A$: Action. Agent의 행동.
• $P(s_{t+1}\mid s_t, a_t)$: Transition probability. 이전 state와 action이 정해졌을 때, state’로 이동할 확률.
• $R(s_t, a_t)$: Reward. State와 action이 정해졌을 때 agent가 받는 보상.
• $\pi(a\mid s)$: Policy. State가 정해졌을 때, agent가 취할 행동의 확률.
• $\gamma$: Discount factor. (value-function에서 설명)

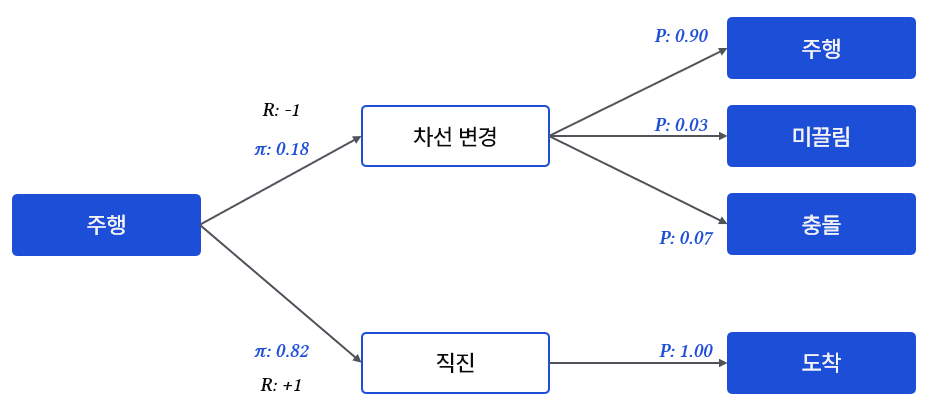
택시 운전 시뮬레이션을 상상해보자.

주행 중인 상태에서 {차선 변경, 직진}이라는 행동을 선택할 수 있다. 보다시피 직진을 해야 목적지에 도착할 수 있기 때문에 학습된 agent는 직진하고 싶어한다. 이처럼 행동을 선택할 확률을 정하는 방법이 policy이다. 차선 변경한 경우를 보면, {주행, 미끌림, 충돌} 등 다양한 상황이 확률적으로 발생할 수 있다. 예시에서는 90% 확률로 주행을 이어가고, 작은 확률로 미끌리거나 충돌할 수 있다. 이러한 확률을 transition probability라고 한다. Agent는 이 확률을 알지 못하며, 행동을 취하고 나온 결과만 관찰할 뿐이다.

MDP를 언급한 이유는 MRP: Markov Reward Process와 많이 혼동하기 때문이다. 실제로 MDP를 검색하면 MRP 이미지가 많이 등장한다. MRP는 ‘Action’이 없다. State에서 바로 state로 이동한다. 따라서 policy도 없고, reward를 받는 위치도 다르다.

MDP에서 각 요소가 무엇을 의미하고, 어디에서 어떤 값을 받는지 이해해야 Value function을 이해할 수 있다.

Value function

Reward는 행동을 취했을 때 즉각적으로 받는 보상이다. Value는 현재 보상 + 예상하는 미래 보상이다. 시험 공부보다 게임을 선택하면 당장의 보상은 더 크지만, 장기적으로 봤을 때는 그렇지 않을 수 있다. 이처럼 미래에 미치는 영향을 생각해 평가한 보상이 Value다.

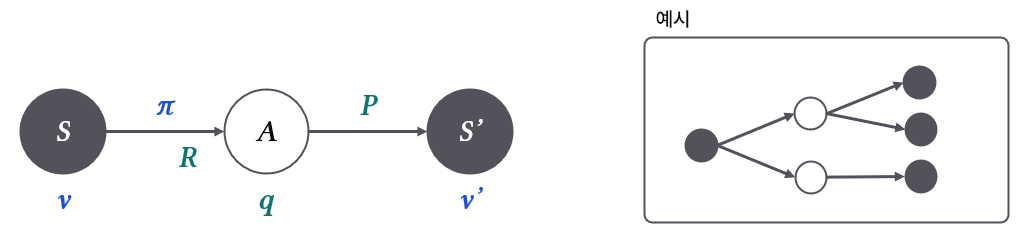
State를 평가할 때는 $v$: state-value를, Action을 평가할 때는 $q$: action-value를 사용한다.

Value는 다음 단계의 가중합으로 생각할 수 있다. $v$는 Reward + 여러 $q$의 가중합으로, $q$는 여러 $v$의 가중합으로 계산한다.

\[v_{\pi}(s) = \sum_{a\in A} \pi(a|s)q_{\pi}(s, a)\] \[q_{\pi}(s, a) = R(s, a) + \gamma \sum_{s'\in S} P(s'|s, a) v_{\pi}(s')\]

$q$는 ‘현재 보상’ + ‘미래 보상’의 형태를 띈다. $\gamma$는 discount factor로 미래에 대한 보상을 얼마나 중요하게 생각할지를 결정한다. $\gamma$가 작으면 당장 눈 앞에 주어진 보상을 중요하게 생각한다. 반대로 $\gamma$가 크면 미래에 있을 큰 보상을 기대하고 움직인다.

앞서 설명했듯 환경을 전부 알면 planning이지 학습은 아니다. 즉, 위에서 정의한 $v$와 $q$는 학습이 아닌 예측에 사용하는 보상 값이다. Planning은 가능한 모든 선택을 반영해 평가하는 반면, Learning은 한 가지 행동을 선택하고, 선택한 결과를 평가한다. 이때 transition probability도 알지 못하기 때문에 훨씬 간단하게 정의된다. 자세한 내용은 Monte-Carlo나 Temporal-Difference라는 주제로 다룬다.