선형 모델과 활성화 함수
선형 구조
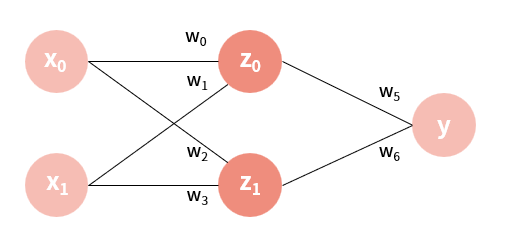
활성화 함수는 알지만 왜 써야하는지 모를 수 있다. 그럼 아래와 같이 은닉층이 있는 신경망은 어떻게 결과값을 계산하는지 확인해보자.
확인을 위해 식을 직접 대입해 보면,
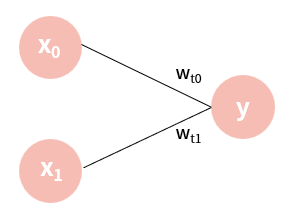
\[y=w_5(w_0x_0+w_1x_1)+w_6(w_2x_0+w_3x_1)\] \[=(w_5w_0+w_6w_2)x_0+(w_5w_1+w_6w_3)x_1\] \[=w_{t0}x_0+w_{t1}x_1\]$w$값들은 그냥 ‘어떤 값’에 불과하다. 따라서, 또 다른 상수로 치환할 수 있다. 결과적으로 레이어를 추가했지만 또 다른 선형 함수가 만들어졌다. 그림으로 나타내면 아래와 같다.
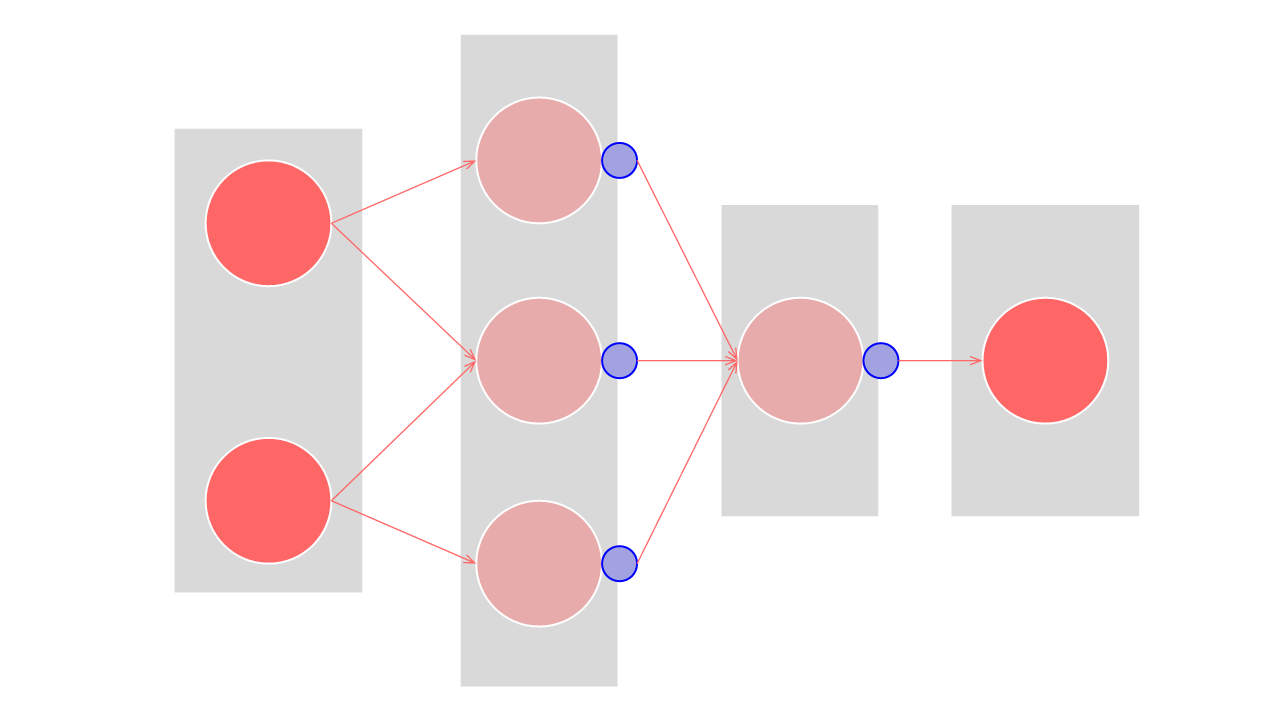
즉, 은닉층을 선형적으로 쌓아도 결국 하나의 선형 함수로 정의된다는 것이다. 따라서 위와 같은 문제를 해결하기 위해 활성화 함수가 필요하다. 선형 모델은 사실상 아래와 같이 활성화 함수(파란점)와 결합된 형태로 사용한다.
활성화 함수
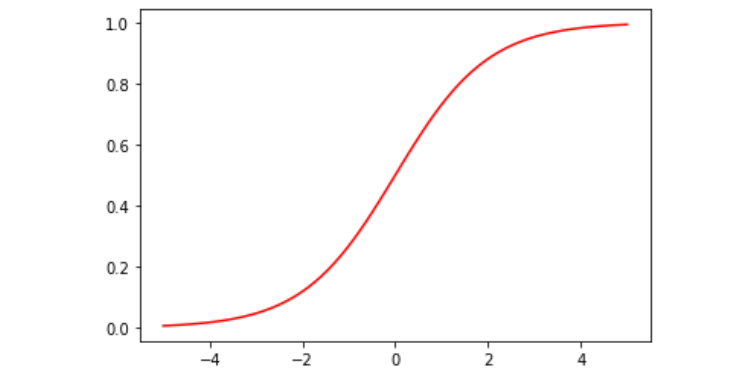
Sigmoid
1
torch.nn.functional.sigmoid()
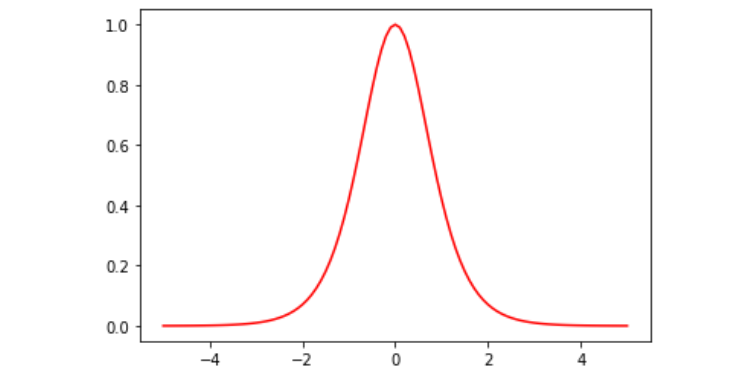
sigmoid는 0 ~ 1 사이의 범위를 가진다는 특징이 있다. 이러한 특징 때문에 이진 분류 문제에서 최종적으로 sigmoid를 거쳐 결괏값이 나오도록 만든다.
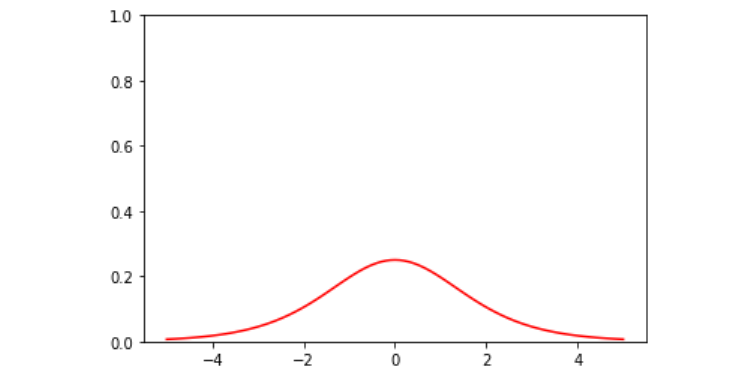
하지만 sigmoid를 잘 사용하지 않는 이유는 기울기 소실(Vanishing Gradient) 현상 때문이다. (여기서부터는 역전파에 대한 이해가 필요하다.) 모델을 학습하는 과정에서 sigmoid의 미분값을 곱하게 되는데, sigmoid를 미분한 형태는 아래와 같다.
최댓값이 $x$가 0일 때 0.25로 매우 작은 값을 가지게 된다. 여러 층을 거쳐 학습을 반복하게 되면 결과적으로 미분 값이 아주 작아진다. 이러한 현상을 Gradient가 소실된다고 표현한 것이다.
tanh
1
torch.nn.functional.tanh()
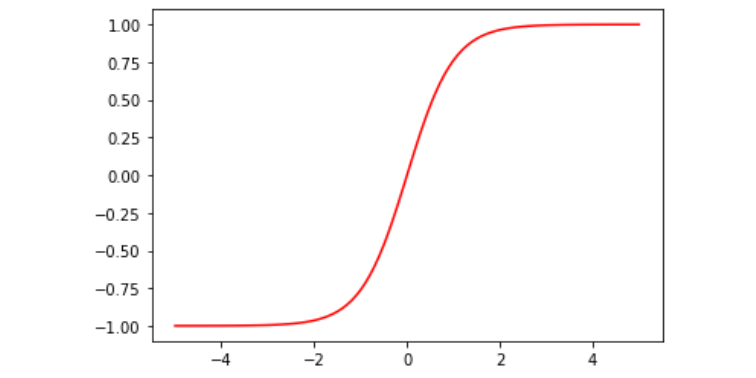
tanh(Hyperbolic Tangent) 함수는 sigmoid에 비해 더 급격한 기울기를 가진다. tanh에서 주목할 부분은 미분값이다.
sigmoid와 달리 0일 때 최댓값으로 1을 갖는다. 하지만 여전히 0에서 멀어지면서 값이 0에 가까워지기 때문에 신경망이 깊다면 기울기 소실 문제가 발생할 수 있다.
ReLU
1
torch.nn.functional.relu()
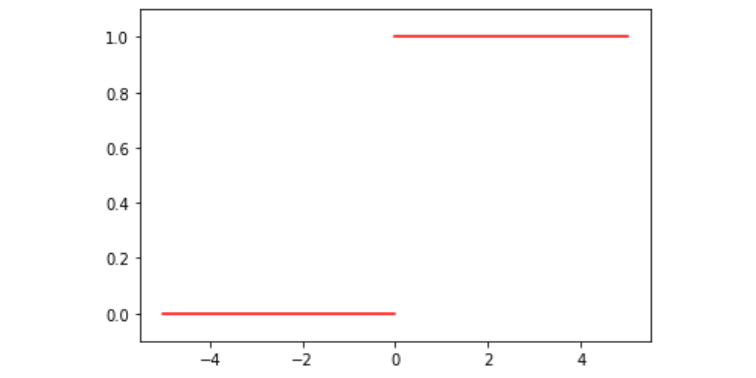
ReLU(Rectified Linear Unit)는 0보다 작은 값을 모두 0으로 처리한다는 특징이 있다. ReLU는 일반적으로 기울기 소실 문제의 대안으로 언급된다.
ReLU는 sigmoid나 tanh의 미분값에서 보였던 문제를 해결하였다. 또 계산이 단순하고 음수를 모두 0으로 처리하기 때문에 연산 효율이 뛰어나다. 문제는 음수값들이 모두 0으로 사라진다는 것이다. 이러한 문제를 Dying ReLU라고 부른다.
ReLU 변형
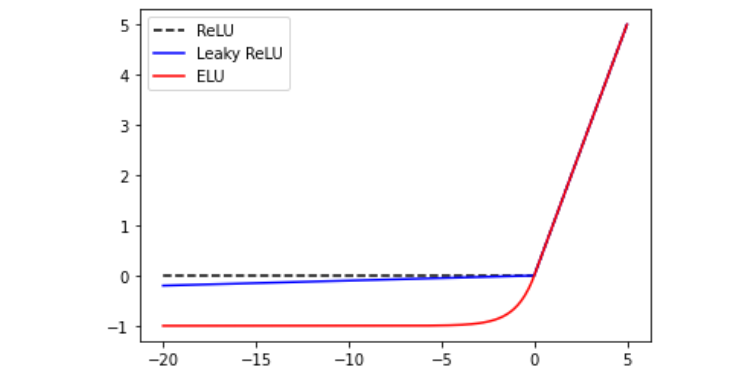
앞에서 봤듯이 ReLU는 장점이 많지만 음수가 0으로 사라지는 문제가 있었다. 이 문제를 해결하기 위한 대안으로 여러 종류의 ReLU가 파생되어 사용되고 있다. 대표적으로 Leaky ReLU와 ELU가 있다.
1
2
torch.nn.functional.leaky_relu(x, negative_slope=0.01)
torch.nn.functional.elu(x)
Leaky ReLU는 0 이하의 값에 대해 작은 기울기(0.01)를 가진다. ELU는 0 이하의 값에 대해 exp함수를 적용해 기울기가 변하도록 조정해 주었다. 하지만 이 함수들도 단점은 있다. Leaky ReLU의 경우, 여전히 선형을 띄고 있고 음수값에 큰 변화가 없기 때문에 성능을 보장하지 않는다. ELU의 경우, 비선형의 형태를 띠지만 exp 함수로 인해 연산 효율이 상대적으로 좋지 않다.
Leaky ReLU와 ELU 외에도 PReLU와 같이 변형된 함수들이 존재한다.