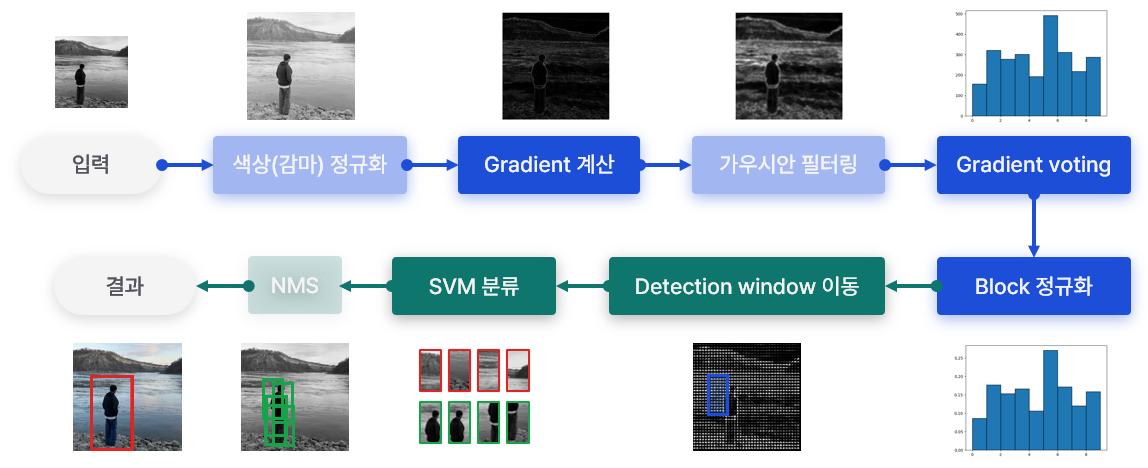
Histograms of Oriented Gradients for Human Detection

Histograms of Oriented Gradients for Human Detection(vision.stanford) 논문을 바탕으로 HOG descriptor 작동 원리에 대해 분석한다. 논문을 완전히 번역하는 것이 아닌 내용을 분석하고 정리한 글이다. 따라서 실제 논문 목차와 다르며, 필자의 설명이 추가되었다.

본 글에서 gradient는 이미지의 x 또는 y 방향에 대한 미분값을 말하며, 자세한 내용은 블로그: edge-detection에서 정의했다. SVM도 블로그: svm에서 다뤘었다.

초록

본 연구는 Linear SVM을 이용한 사람 검출 모델을 개발했다. 이미지 gradient를 이용해 경계(edge)를 탐지하는 Histograms of Oriented Gradient(HOG) descriptor는 사람 검출에 매우 좋은 성능을 보였다.

• fine-scale gradients: 픽셀 간 gradient 크기 계산
• fine orientation binning: 방향 정보를 히스토그램 bin으로 사용
• relatively coarse spatial binning: 인접한 픽셀을 “Cell” 단위로 묶어서 계산
• high-quality local contrast normalization: “Block” 단위 정규화

주요 특징은 위와 같으며, 자세한 내용은 본문에서 소개한다.

요약

객체 부분 특징은 gradient 크기(magnitude)와 방향(orientation)으로 나타낼 수 있다. 본 연구는 Cell이라는 단위로 공간을 나누어 계산한다. 각 cell에 대해 gradient 히스토그램을 생성한다. 그리고 Block이라는 더 큰 단위로 묶어 정규화를 진행한다. 이렇게 정규화된 block을 HOG descriptor라고 한다.

참고로 cell은 픽셀을 n x n으로 묶은 단위이며, block은 cell을 m x m으로 묶은 단위다. 위 예시는 8 x 8 픽셀의 cell과 2 x 2 cell을 묶은 block이다.

HOG는 경계와 gradient 구조를 잘 파악한다. 또 약간의 이미지 변환(왜곡, 회전 등)에도 강하다. 사람 탐지 문제에서는 넓은 범위의 정규화가 도움이 된다. 이는 사람이 서있는 모습은 유지한 상태로 팔다리를 앞뒤로 움직이기 때문으로 보인다. 다시 말해, 큰 형태는 유지한 채 작은 변화가 발생하기 때문에 넓은 공간에 대한 일반화는 모델 성능에 영향을 준다.

구현 및 성능

각 단계에 대해 설명하고 모델 성능에 끼치는 영향을 분석한다. 본론에 앞서 기본(default) 모델은 다음과 같이 정의한다.

• RGB 색상 공간에 대해 gamma 보정 없음
• [-1 0 1] 필터를 보정(smoothing) 없이 사용
• voting 전, $\sigma = 8$의 가우시안 필터를 cell 단위로 적용
• 히스토그램이 방향 정보 0° ~ 180°에 대해 9개 bin을 가지도록 구성
• block은 16 x 16으로 4개의 8 x 8 cell로 구성
• block에 대해 L2-Hys(Lowe-style clipped L2norm) 정규화
• 정규화 시, block은 8 픽셀의 stride를 가짐 (4-fold coverage)
• 64 x 128 detection window
• Linear SVM

감마/색상 정규화

Power law (gamma) equation을 이용해 이미지 정규화를 시도했다.

• 컬러 이미지를 보정했을 때 약간의 성능 향상을 보였다. 이후 단계에서 정규화를 따로 진행하기 때문에 큰 효과가 없는 것으로 보인다.
• 회색조 이미지는 1.5% 성능이 감소했다.

추가로 square root gamma compression은 1%의 성능 향상을 보였지만, log compression은 너무 강한 나머지 2% 성능 하락을 보였다.

Gradient 계산

가우시안 필터를 이용한 smoothing과 다양한 마스크(cubic-corrected, sobel, diagonal 등)를 실험했다. 가우시안 필터를 사용하지 않고($\sigma=0$), [-1 0 1] 마스크를 적용했을 때 가장 좋은 성능을 보였다.

Smoothing은 성능에 치명적이다. $\sigma$를 0에서 2로 늘렸을 때, recall rate가 89%에서 80%으로 감소했다.

큰 마스크를 사용했을 때 성능이 감소했다. [-1, 1] 마스크도 1.5% 성능이 감소했는데, x와 y 방향에 대해 중심이 같지 않기 때문에 발생한 것으로 추측된다. 다시 말해, 계산하는 픽셀에 대해 대칭인 마스크가 아니기 때문에 gradient(변화)를 잘 반영하지 못한 것으로 보인다.

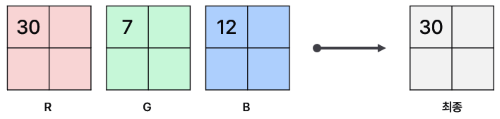
컬러 이미지는 각 채널에 대해 gradient를 구한다. 각 픽셀에 대해 3개 채널의 gradient 중 norm(크기)이 가장 큰 벡터를 최종 gradient로 채택한다. 이는 각 채널(색상) 중 가장 강한 특징을 gradient(변화율)로 사용하기 위해서다.

방향 binning

히스토그램에서 각 막대의 구간을 bin이라고 하며, 데이터 분포에 맞게 bin을 나누는 과정을 binning이라고 표현한다. 나누어진 bin에 대해 데이터를 축적하는 과정은 voting이라고 한다.

본 모델은 각 gradient 방향을 bin(x축)으로 설정하고, gradient 크기를 막대(y축)에 축적한다. 이러한 히스토그램을 cell마다 생성한다.

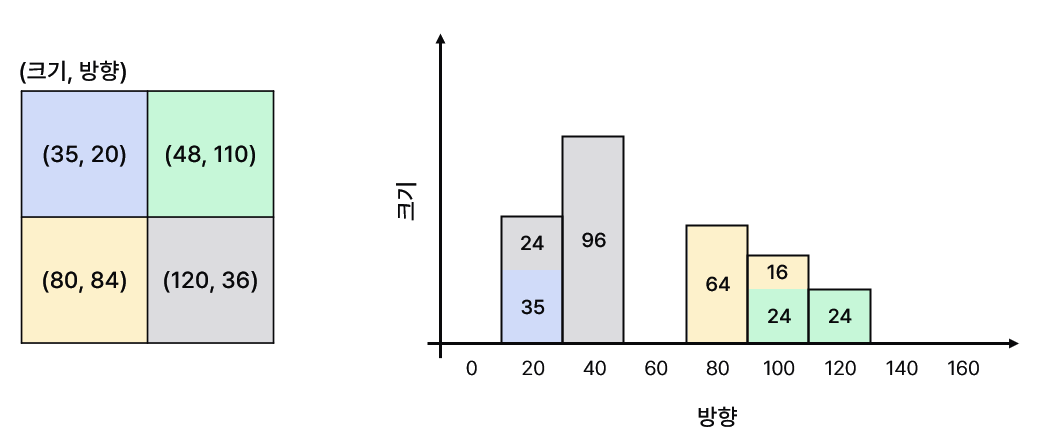
bin은 0° ~ 180°(unsigned) 또는 0° ~ 360°(signed)에 대해 균일하게 나눈다. 예를 들어, unsigned 방향에 대해 9개 bin을 지정한다면 [0°, 20°, 40° … 160°]가 된다. 만약 현재 픽셀의 방향 정보가 105라면 가장 가까운 100 구간으로 분류할 수 있다. 하지만 이는 aliasing을 만든다. 따라서 더 정교한 분류를 위해 bilinear interpolation을 사용한다.

4개의 픽셀에 대해 히스토그램을 생성하는 예시다. 초록 픽셀(48, 110)을 살펴보자. 110은 100과 120 사이의 값이다. 100으로부터 10만큼 떨어져있고, 120으로부터 10만큼 떨어져있다. 따라서 거리를 기반으로 가중치를 주어 100과 120에 gradient를 나누어 줄 수 있다.

• 100° 구간: $48\times \cfrac{|100-110|}{20}$
• 120° 구간: $48\times \cfrac{|120-110|}{20}$

따라서 100과 120에 각각 24를 나누어주는 방식으로 히스토그램을 완성한다. 다른 셀도 같은 방식으로 gradient 크기를 축적한다.

gradient 크기는 기본(L2-norm), square, square root 등 다양한 방식으로 정의할 수 있지만 기본 L2-norm이 가장 좋은 결과를 보였다.

bin 개수를 늘리는 것은 9개까지 유의미한 성능 향상을 보였다. 9개 이상은 큰 차이를 발견하지 못했다. 이는 bin을 unsigned 방향에 대해 나누었을 때 이야기다. signed 방향으로 나누는 것은 오히려 성능을 떨어뜨린다. 사람 탐지에서는 옷 색상, 배경 등 폭넓은 정보를 다루기 때문에 signed 정보가 의미없을 수 있다. (참고로 다른 객체에 대해서는 signed가 좋은 모습을 보일 수 있다.)

정규화

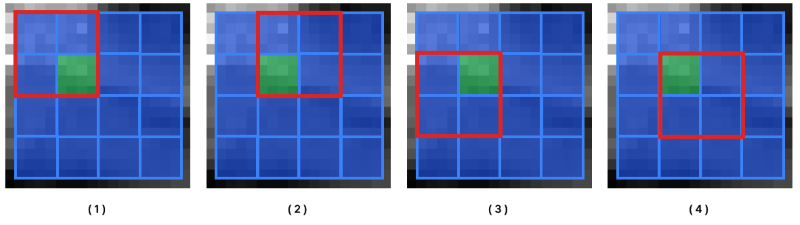
정규화는 성능에 큰 영향을 준다. cell을 block 단위로 묶어 정규화를 진행한다. 정규화에서 stride를 사용해 cell이 겹치도록 할 경우, 성능이 크게 올라간다. 예를 들어, 16 x 16 블록을 8 픽셀 씩 겹치도록 정규화를 수행할 경우 한 cell은 4번의 정규화에 사용된다. 이를 4-fold coverage라고 표현한다. 아래 그림을 보면 쉽게 이해할 수 있다.

빨간 테두리는 현재 단계에서 정규화가 진행되고 있는 block 크기의 구역을 나타낸다. 초록 색으로 표현한 cell은 총 4번의 정규화에 영향을 준다. 다른 cell도 중복으로 총 4번의 정규화에 사용된다.

정규화 방법은 총 4 종류를 실험했다. 정규화하지 않은 벡터를 $v$라 할 때,

L2-norm: $\cfrac{v}{\sqrt{| v |_2^2+\epsilon^2}}$

L2-Hys: $max(L2(v), 0.2)$

L1-norm: $\cfrac{v}{| v |_1+\epsilon}$

L1-sqrt: $\cfrac{v}{\sqrt{| v |_1+\epsilon}}$

L2-Hys, L2-norm, L1-sqrt는 비슷한 성능을 보였고, L1-norm은 성능이 5% 감소했으며, 정규화를 수행하지 않으면 성능이 27% 감소했다.

Block 단위의 정규화 대신 Centre-surround 정규화도 시도해봤다. 방향에 대한 합계(히스토그램)에 가우시안 필터를 통해 정규화하는 방식이다. $\sigma= 1$ cell width로 수행했을 때 2% 성능 하락이 있었다. 이 방법은 각 셀 안에서 필터를 적용하는 방식으로 block 간 겹치는 현상이 없기 때문이다. 이를 통해 다른 공간에 있는 상대적인 정보를 반영하는 것이 더 중요하다는 것을 알 수 있다.

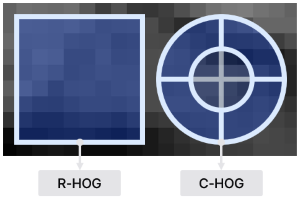
R-HOG와 C-HOG

Block 모양을 정의하는 방법에 따라 R-HOG와 C-HOG로 나뉜다.

R-HOG: Radial HOG는 정사각형의 n x n 크기를 하나의 셀로 정의한다. 사람 탐지 문제에서 6 x 6 픽셀의 cell과 3 x 3개 cell로 이루어진 block이 가장 좋은 성능을 보였다. 학습에 사용한 이미지에서 사람의 신체(손, 다리 등)가 약 6 ~ 8 픽셀 정도였기 때문이다. 2 x 2나 3 x 3 블록은 효과가 좋았으나, 너무 크거나 작은 블록은 특징을 과하게 또는 작게 반영해 성능이 좋지 않았다.

Gradient에 대해 가우시안 필터($\sigma=0.5$ * block width)를 적용한 뒤 vote하면 1% 성능 향상을 보인다. 참고로 이미지 픽셀에 대해 smoothing을 적용하는 것이 아니라 계산한 gradient 크기에 대해 필터를 적용하는 것이다. 따라서 객체 경계를 흐릿하게 만드는 일반적인 smoothing filter와 다르다.

다양한 크기의 cell과 block을 사용하는 방식은 미미한 성능 향상을 보였지만 descriptor 크기를 크게 증가시킨다.

vertical(2x1) block과 horizontal(1x2) block보다는 둘을 같이 사용하는 편이 낫지만, 여전히 2 x 2와 3 x 3 block이 더 좋다.

C-HOG: Circular HOG는 원 형태의 block으로 중심이 여러 개의 angular sector로 구분되어 있다. 총 4개의 파라미터를 가진다.

• angular bin 개수
• radial bin 개수
• 중심 bin 반지름
• expansion factor

최소 2개의 radial bin과 4개의 angular bin을 사용해야 좋은 성능을 보인다. radial bin을 늘리는 것은 큰 차이를 만들지 못하고, angular bin을 늘리는 것은 오히려 성능을 낮춘다.

중심 반지름에 대해 4 픽셀이 가장 좋은 성능을 보였다.

Detection window

계산된 descriptor는 SVM에 입력되기 전 detection window로 조각조각 나누어진다.

64 x 128 크기의 window는 16 픽셀의 여백(margin)을 포함한다. 여백을 16에서 8로 변경하면 4%의 성능이 감소한다. window 크기를 유지하고 내부 사람을 키울 때도 성능이 감소한다. 필자가 이미지를 이용해 테스트 해보니 사람 주변에 충분한 여백이 없다면 사람을 찾지 못한다.

분류

기본으로 $C=0.01$인 soft linear SVM을 사용한다. Gaussian 커널을 사용한 SVM의 성능이 3% 정도 더 좋지만 실행 시간(runtime)이 크게 늘어난다.

결과 비교

MIT와 INRIA 데이터셋에 대해 아래 모델과 비교를 진행했다.

• Generalized Haar Wavelets
• PCA-SIFT
• Shape Contexts

대체적으로 타 모델에 비해 우수한 성적을 보였다. MIT 데이터셋에 대해 완벽에 가까운 성능을 보였다. INRIA 데이터셋에 대해서도 False positive per window가 유의미하게 감소했다.

R-HOG와 C-HOG는 비슷한 성능을 보였지만 C-HOG가 약간 더 좋았다. R2-HOG(primitive bar detector가 추가된 R-HOG)는 2% 정도 성능 향상을 보였다. Binary edge voting(EC-HOG)은 C-HOG에 비해 5% 정도 성능이 감소했다. Gradient 방향을 생략하고 계산하면 성능이 33% 하락한다.

코드로 정리하기

자세한 구현 코드는 Github: hog에서 확인할 수 있다.

CELL_SIZE = 8  # Cell: 8 x 8 pixel
BLOCK_SIZE = 2  # Block: 16 x 16 pixel
BLOCK_STRIDE = 1  # 4-fold coverage
STD = 8  # Block_width * 0.5
N_BINS = 9
UNSIGNED = 180

# 이미지 준비
image = cv2.imread("human.jpg", cv2.IMREAD_GRAYSCALE)

# Gradient 크기 및 방향
magnitude, orientation = gradients(image)

# Gaussian 필터 적용
filtered_magnitude = gaussian_filter(magnitude, CELL_SIZE, BLOCK_SIZE, STD)

# Histogram 생성
hist = vote_histogram(filtered_magnitude, orientation, CELL_SIZE, N_BINS, UNSIGNED)

# Block 정규화
norm_hist = normalize(hist, BLOCK_SIZE, BLOCK_STRIDE)

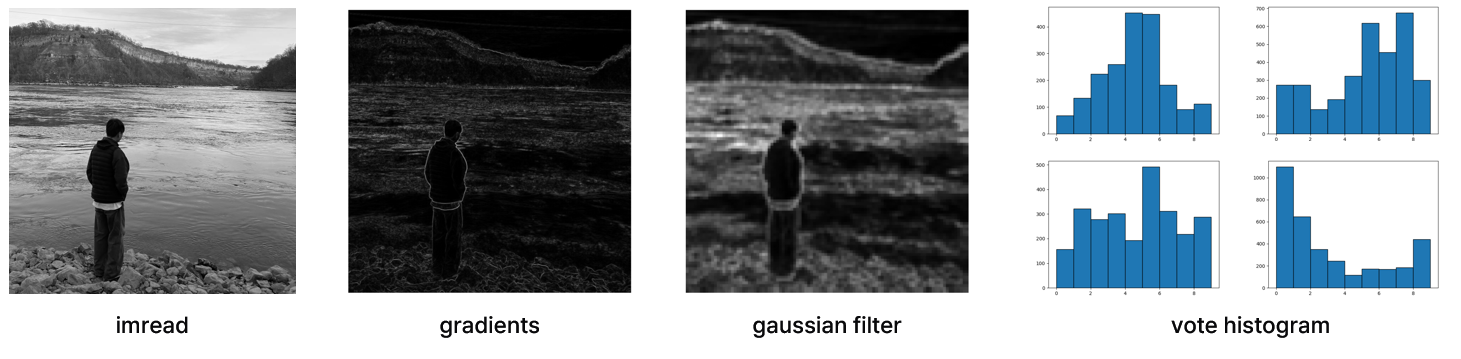
기본 HOG descriptor를 코드로 정리했다. 각 단계의 결과를 시각화하면 다음과 같다.

학습된 OpenCV의 HOG 모델을 이용해 추론하면 원하는 결과를 잘 찾는다. 자세한 코드는 Github: detection.cpp에 있다.

HOGDescriptor hog;
hog.setSVMDetector(HOGDescriptor::getDefaultPeopleDetector());

vector<Rect> detected;
hog.detectMultiScale(img, detected, 0, Size(8, 8), Size(16, 16));

시각화

skimage는 scikit-learn image로 HOG 특징을 쉽게 시각화할 수 있는 함수를 제공한다.

features, hog_image = hog(
    image,
    orientations=9,
    pixels_per_cell=(8, 8),
    cells_per_block=(2, 2),
    visualize=True,
)

# 시각화를 위한 Normalize
hog_image = exposure.rescale_intensity(hog_image, in_range=(0, 10))