Optimizer 살펴보기

게시 2023/01/05

By 박성진

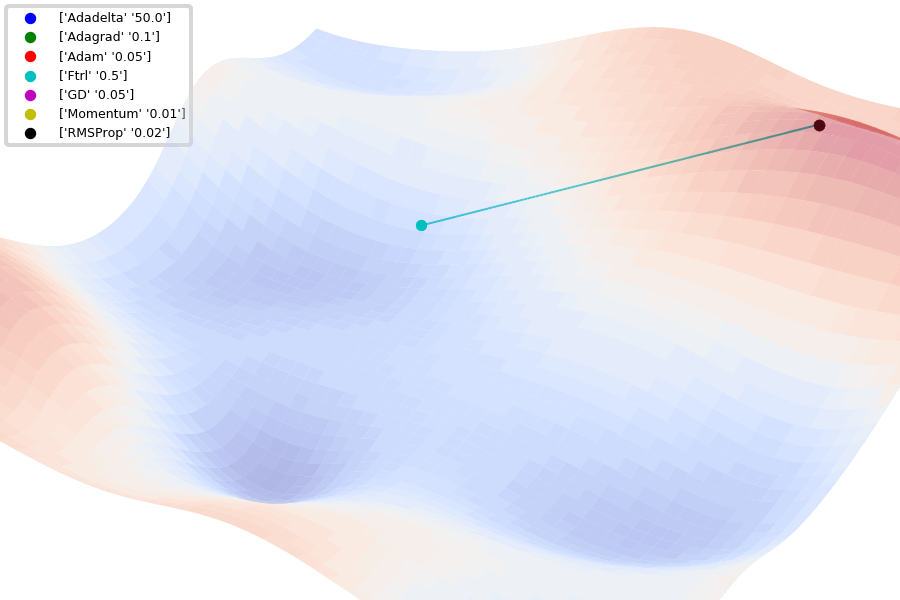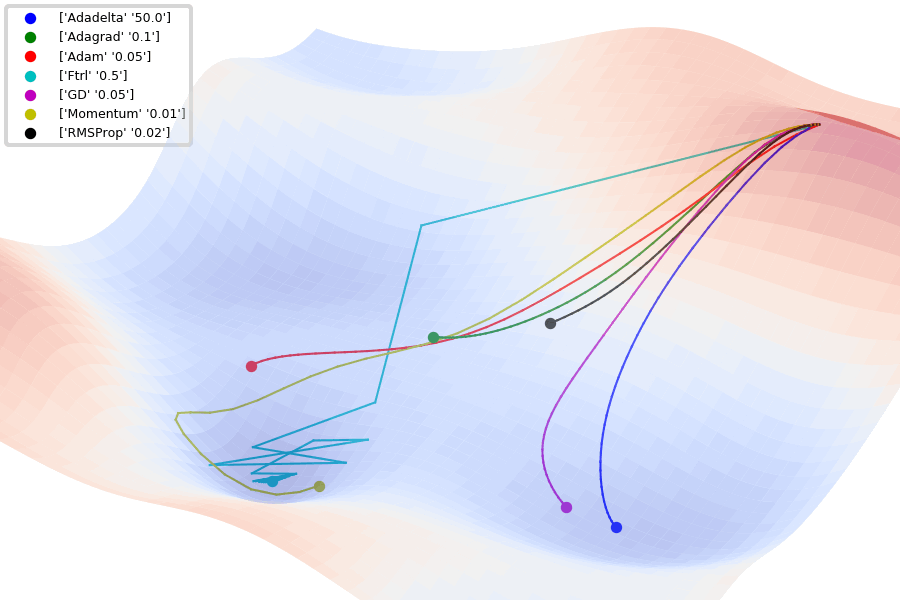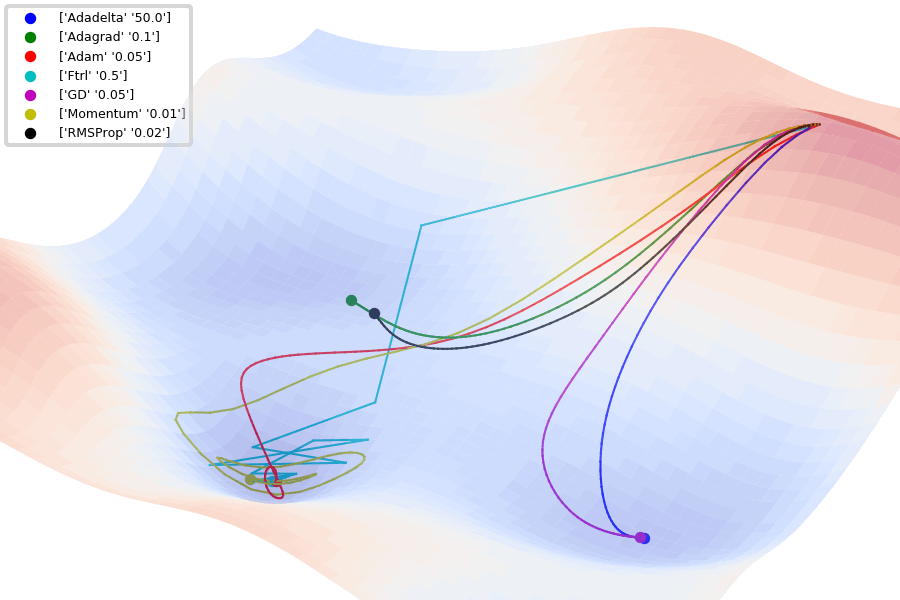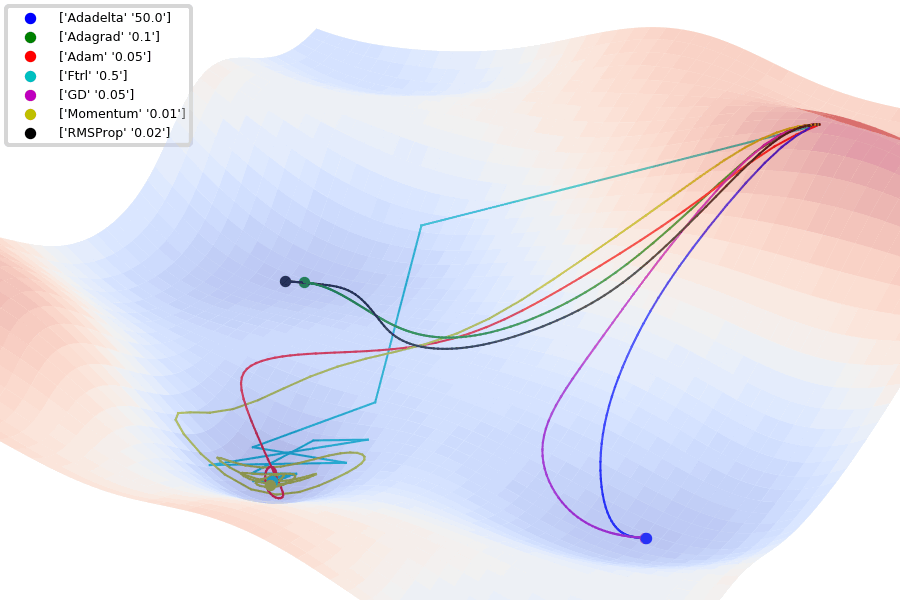Jaewan-Yun: optimizer-visualization

Optimizer는 모델의 Training Loss를 최소화하는 방향으로 파라미터를 업데이트하는 중요한 역할을 한다. 쉽게 말해 모델을 어떤 방향으로 얼마만큼 업데이트할 것인지를 결정하는 역할을 한다. Optimizer는 Gradient Descent(경사하강법)를 기반으로 한다. 기울기(Gradient)는 학습 방향을 결정하고, 학습률은 학습할 정도를 결정한다. 여기까지 내용을 모른다면 “경사하강법과 학습률“을 먼저 이해해야 한다.

아래 내용은 Gradient Descent를 기반으로 한 여러 optimizer의 개념들을 설명한다.

기호 정리

$w$: 가중치
$t$: 시점(step)
$\mu$: 학습률
$L$: Loss 값

SGD

SGD는 Stochastic Gradient Descent의 약자로 각각의 데이터를 반영해 가중치를 업데이트한다. 기본적인 경사 하강법은 전체 데이터를 살펴 본 후, 한 번에 가중치를 업데이트한다. 그에 반해 SGD는 각각의 데이터를 보고 학습을 진행하기 때문에 더 빠른 학습이 가능하다. 하지만 그만큼 노이즈에 민감할 수 있다는 단점도 있다.

\[w_t=w_{t-1}-\mu\cfrac{dL}{dw}\]

주의할 점은 일반적으로 SGD라고 하면 Mini-batch Gradient Descent를 뜻한다. 이름 그대로 미니 배치의 데이터를 확인한 후, 가중치를 업데이트하는 방식이다. Pytorch의 SGD를 이용해 학습할 때는 Mini-batch Gradient Descent의 개념을 가지고 있으며, 아래에서 소개할 momentum도 적용할 수 있다.

momentum

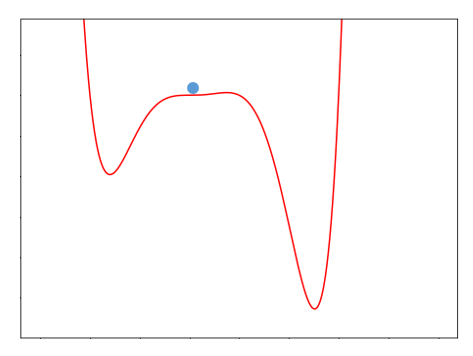
경사 하강법의 saddle point(안장점) 문제를 가지고 있다. 안장점 문제란 최솟값은 아니지만 기울기가 0에 가까워서 업데이트되지 않는 상황을 뜻한다. 이러한 문제를 해결하기 위해 도입된 개념으로, momentum(관성)은 물체가 운동하는 추세를 뜻한다.

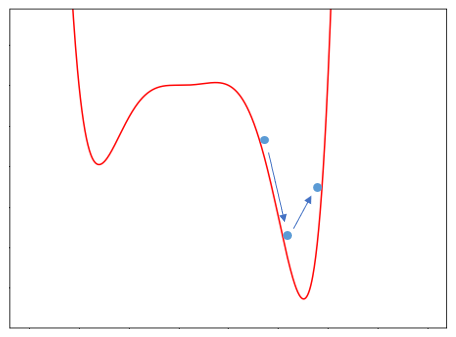
Gradient의 위치를 보면 기울기가 거의 0에 가깝다. 따라서 0에 가까운 아주 작은 값이 업데이트되면서 마치 학습이 멈춘 것처럼 보이게 된다. 이런 상황을 안장에 안착하였다고 해서 안장점 문제라고 한다. 본론으로 돌아가서 momentum은 마치 공에 관성이 있는 것처럼 값이 움직이는 것을 말한다.

\[v_t=\gamma v_{t-1}-\mu\cfrac{dL}{dw}\] \[w_t=w_{t-1}+v_t\]

미분 값을 활용하여 업데이트하는 것이 아니라 누적된 $v$값도 함께 적용된다. 따라서 만약 이전의 기울기가 현재의 기울기와 같은 방향이라면 관성이 적용된다. $\gamma$는 관성 계수로 0 ~ 1 사이의 값을 가지며 $v_0$는 0으로 초기화된다. 일반적으로 관성 계수로 0.9가 많이 사용한다.

  
import torch.optim as optim

optimizer = optim.SGD(model.parameters(), lr=LEARNING_RATE, momentum=0.9)

for epoch in range(n_epochs):
    for x, y in dataloader:
        # 생략...
    
        optimizer.step()

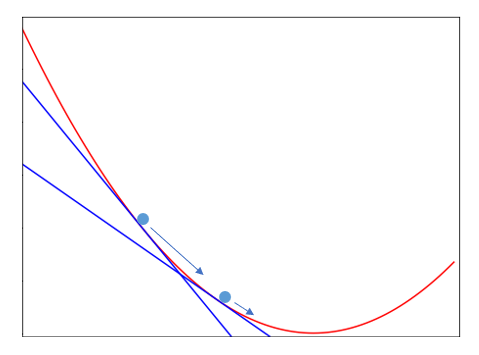
문제는 가파른 구간에서 over shooting 문제 발생한다. 이전 기울기가 가파르다면 현재의 기울기가 작아져도 관성이 적용되어 원래보다 크게 움직이게 된다. 그러면 아래처럼 최솟값을 지나치는 문제가 발생할 수도 있다.

Adagrad

momentum에서 over-shooting 문제가 발생한 것은 현재의 기울기 상태를 적게 반영했기 때문이다. Adagrad는 현재 기울기가 커지면 학습률을 ‘상대적으로’ 줄여주고, 반대로 현재 기울기가 커지면 학습률을 상대적으로 늘려주는 기능을 가진다.

\[h_t=h_{t-1}+\cfrac{dL}{dw}\odot \cfrac{dL}{dw}\] \[w_t=w_{t-1}-\cfrac{\mu}{\sqrt{h_t}+\epsilon}\times\cfrac{dL}{dw}\]

$\odot$은 행렬의 원소별 곱을 뜻한다. 즉, $h$는 가중치 변화율의 제곱을 더해 계산된다. 기울기에 제곱을 하게 되면서 방향이 아닌 기울기의 크기에 집중하였다. 기울기의 크기가 커지면 $h$가 증가하면서 최종적으로 학습률은 감소한다. 반대로 기울기의 크기가 작아지는 구간에서는 $h$가 감소하며 상대적으로 학습률이 증가하는 효과를 얻을 수 있다.

하지만 학습이 진행됨에 따라 $h$값이 계속 누적하여 증가하게 되고, 최종적으로 학습률이 0에 가까워진다. 이렇게 되면 더 이상 학습이 진행되지 않는 문제가 발생할 수 있다.

RMSProp

Root Mean Sqaure Propagation, 줄여서 RMSProp이라고 부르는 기법은 Adagrad에 지수가중이동평균을 적용하였다. 쉽게 말해 $h$에 무작정 값을 누적하는 것이 아니라 이전 상태와 현재 상태에 반영 비율을 적용해 주는 것이다.

\[h_t=\gamma h_{t-1}+(1-\gamma)\cfrac{dL}{dw}\odot \cfrac{dL}{dw}\] \[w_t=w_{t-1}-\cfrac{\mu}{\sqrt{h_t}+\epsilon}\times\cfrac{dL}{dw}\]

이전 상태의 정보를 담고 있는 $h_{t-1}$은 $\gamma$만큼 반영하고, 현재 미분 값의 제곱은 $(1-\gamma)$만큼 반영하여 새로운 $h$를 구한다. 그리고 Adagrad와 같은 원리로 계산한다.

이를 통해 Adagrad처럼 $h$가 커지는 현상을 완화했다. 하지만 그만큼 이전 상태를 덜 반영하게 된다. 눈치챘겠지만 RMSProp을 개선한 버전이 다음에 소개할 Adam이다.

Adam

momentum + RMSProp의 개념을 적용한 것이 Adam이다.

\[m_t=\beta_1 m_{t-1}+(1-\beta_1)\cfrac{dL}{dw}\] \[\hat{m_t}=\cfrac{m_t}{1-\beta_1}\] \[v_t=\beta_2 v_{t-1}+(1-\beta_2)\cfrac{dL}{dw}\odot\cfrac{dL}{dw}\] \[\hat{v_t}=\cfrac{v_t}{1-\beta_2}\] \[w_t=w_{t-1}-\mu\cfrac{\hat{m_t}}{\sqrt{\hat{v_t}}+\epsilon}\] \[m_0=0, v_0=0\]

위 식에서 $m$을 계산한 과정은 momentum을 계산하는 식과 동일하다. $v$를 구하는 과정은 RMSProp과 동일하다. $\hat{m}$과 $\hat{v}$를 계산하는 과정은 bias correction이라고 한다. bias correction과 관련된 자료는 아래 링크를 참조하자.

bias correction 설명: youtu.be/lWzo8CajF5s
Adam에서 correction을 하는 이유: stats.stackexchange.com/questions

가장 많이 사용되는 값은 $\beta_1=0.9$, $\beta_2=0.999$, $\epsilon=10^{-8}$이다.

  
import torch.optim as optim

optimizer = optim.Adam(model.parameters(), lr=LEARNING_RATE)

추가로 Adam의 변형된 버전인 AdamW, NAdam 등도 있다.

가장 널리 사용되는 optimizer는 Adam이다. Adam을 사용하면 보편적으로 나쁘지 않은 성능을 보인다. ~~교수님이 안 되면 일단 Adam 써보라고 하셨을 정도.~~ 클래식한 SGD + momentum도 종종 사용된다. Pytorch에서는 optim을 통해 사용할 수 있다.

Pytorch AI

SGD

momentum

Adagrad

RMSProp

Adam

인기 태그