글

경사하강법과 학습률

게시
By 박성진

사전 지식

  • 평균 ( $\cfrac{1}{n} \sum_{i=1}^{n}x_i$ )
  • 이차함수의 미분과 접선의 기울기
  • 편미분

전체 개념 살펴보기

여기서 이해 못 해도 괜찮다. 일단 읽고 넘어가자.

딥러닝에서 모델을 학습한다는 것은 실제 값과 예측 값 오차를 최소화하는 가중치를 찾는 과정이다. 여기서 ‘오차’를 정의하는 함수를 비용 함수(Cost function)라고 한다. 즉, 비용 함수(오차)가 최솟값을 갖는 방향으로 가중치를 업데이트해야 한다.

경사 하강법이라고 불리는 Gradient Descent는 최솟값을 찾을 때 사용할 수 있는 최적화 알고리즘이다. 먼저, 최솟값을 찾을 함수를 설정한 후, 임의의 값으로 초기화한다. 그리고 기울기를 빼면서 최솟값에 가까워질 때까지 반복하는 방법이다.

\[w^{t+1}=w^t-\mu\cfrac{dE(w)}{dw}\]

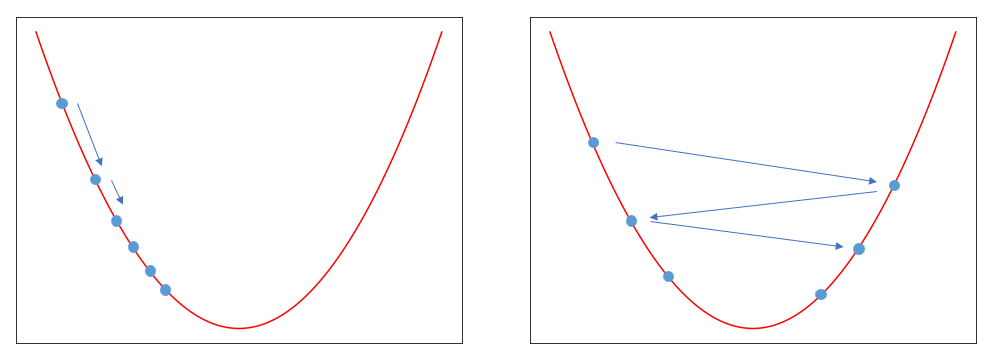
$E(w)$는 오차를 계산하는 비용 함수(목적 함수)이며, $w$는 오차를 구하는 과정에서 사용된 가중치이다. $t$ 시점의 $w$에 대해 편미분한 값을 빼서 $t+1$ 시점의 $w$를 구하는 과정을 식으로 나타낸 것이다. 미분 값 앞에 곱해져 있는 상수는 학습률(learning rate)이다. 학습률이 작으면 왼쪽 그래프처럼 값이 천천히 변하고, 학습률이 크면 오른쪽 그래프처럼 큰 보폭으로 움직인다. 

용어 정리: 오차를 구하는 함수를 비용 함수라고 소개했다. 이 비용 함수를 최적화하는 것이 목적으로 설정되었다. 따라서 최적화 단계에서는 비용 함수라는 용어 대신 목적 함수라는 표현을 사용한다. 위에서는 이해를 위해 비용 함수로 작성했지만 엄밀히 말하면 목적 함수가 정확한 표현이다. 자세한 내용은 뒤에서 계산하며 확인할 수 있다.

경사하강법을 쉽고 자세하게

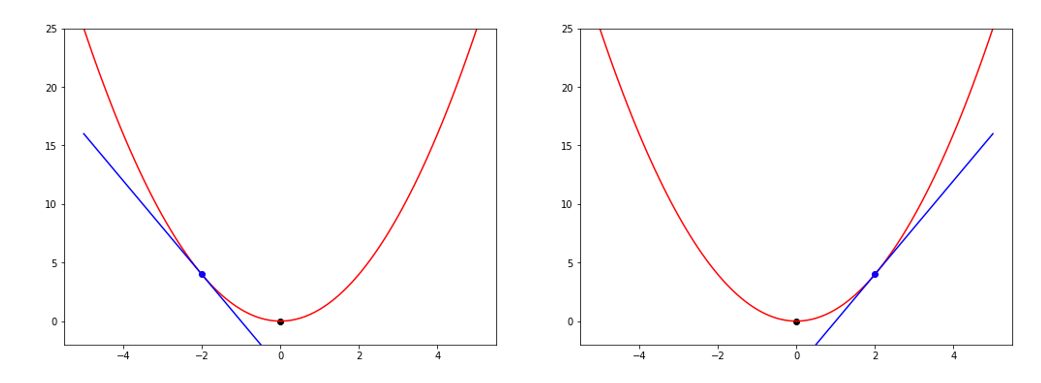
아래 그림처럼 점 하나(파란점)를 그래프 위에 찍어보자. 최솟값은 그래프에서 가장 작은 값(검정점)이다. 미분 값이란 현재 점에 대한 그래프의 접선의 기울기이다. (파란선의 기울기)

  • 만약 현재 값이 최솟값의 왼쪽에 있다면 기울기(미분 값)가 음수이기 때문에 현재 값 - 미분 값(음수)를 하면 커지게 된다. 즉, 오른쪽으로 점이 이동한다.
  • 만약 현재 값이 최솟값의 오른쪽에 있다면 기울기가 양수이기 때문에 현재 값 - 미분 값(양수)를 하면 현재 값은 작아지게 된다. 즉, 왼쪽으로 이동하게 된다.
  • 그러다가 최솟값에 도달하면 미분값이 0이 되어 현재 값 - 0으로 더 이상 변화하지 않고 멈춘다. 

따라서 경사 하강법을 적용하면 최솟값 왼쪽의 값은 점점 오른쪽으로 이동하고, 최솟값 오른쪽의 값은 왼쪽으로 이동하게 된다. 이 과정을 계속 반복하면 결국 최솟값에 도달하게 되는 원리이다.

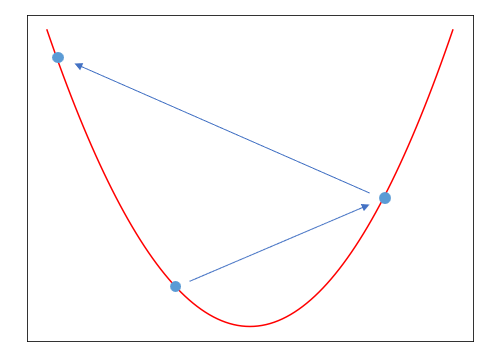
그런데 단순히 미분값만 뺀다고 최솟값에 도달하지는 않는다. 간단하게 그림으로 그려보면 좌우로 움직였지만 오히려 최솟값에서 더 멀어지는 경우다. 이 과정을 반복하면 값이 저 멀리로 날아가 버린다. 

따라서 미분 값은 오직 방향만 결정한다. 왼쪽으로 갈지 오른쪽으로 갈지만 결정한 후, 얼마나 움직일지는 학습률이 결정한다. 

학습률을 쉽고 자세하게

학습률인 learning rate는 학습을 진행할 강도를 결정한다. 여기서 학습한다라는 것은 오차의 최솟값을 찾는다는 의미임을 잊지 않아야 한다. 이 개념을 가지고 아래 예시를 천천히 읽어보자.

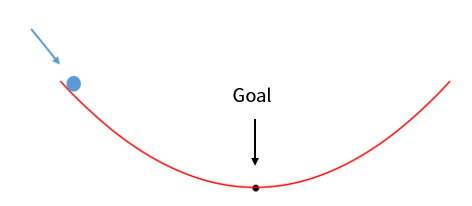
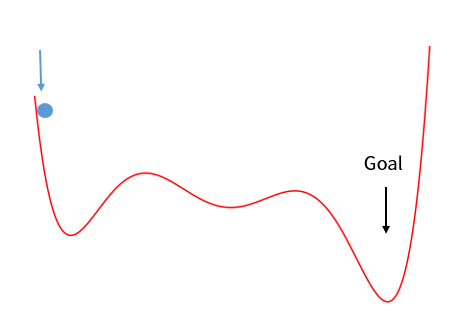
위 그림처럼 생긴 경사면에서 공을 굴려 검은색 포인트에서 멈추도록 하는 게임을 해보자. 여기서 공을 강하게 밀면 좌우로 요동치다가 어느 순간 점점 목적지에 가까워지며 멈출 것이다. 약하게 밀면 주르륵 흘러서 목적지에 도착할 것이다. 하지만 너무 강하게 밀면 공이 튕겨져 나가서 목적지에 도달하지 못할 것이다. 따라서 공을 어느 정도로 강하게 밀지가 관건이다. 

아까 위에서 수식과 함께 봤던 그래프다. 공이 굴러가는 모습을 순간순간 사진으로 찍었다고 생각하면 위와 같이 공이 움직이는 모습을 상상해볼 수 있다. 학습률은 공을 얼마나 세게 밀 것인가와 비슷한 개념이다. 학습률이 너무 크면 값이 튀어 최솟값을 찾지 못한다. 반면 학습률이 너무 작으면 최솟값에 도달하기까지 너무 오래 걸릴 수 있다. 그리고 학습률이 너무 작아서 최솟값을 찾지 못하는 상황도 존재한다. 

똑같은 게임이지만 더 복잡한 맵을 가지고 왔다. 우리가 찾고 싶은 최솟값은 오른쪽 끝에 위치한다. 만약 공을 아주 약하게 민다면 첫 번째 골짜기에 빠져서 멈춰버린다. 공을 애매하게 밀면 두번째 골짜기에서 멈춰버릴 수도 있다. 

이걸 조금 더 있어 보이게 표현하면 Local optimum에 빠진다고 한다. 첫번째 골짜기에 빠져도 부분적으로는 최솟값을 찾은 게 맞다. 하지만 전체에서 최적의 값인 Global optimum을 찾고 싶다. 전역 최솟값이라는 뜻에서 Global minimum이라고도 한다. 

Global optimum을 찾는 방법은 적당히 세게 미는 것이다.

‘적당한’ 학습률은 정해져 있지 않다. 여러 번 밀어 보면서 값을 키우거나 줄여서 적당한 값을 찾아가는 수밖에 없다. 그래서 어떤 논문에서는 학습률이 0.1일 때, 0.01일 때, 0.001일 때… 이런 식으로 기록해 둔 것도 본 적이 있다. 대중적인 모델의 경우, ‘대충 어느 정도의 학습률이 좋더라’와 같은 정보를 논문 또는 구글링으로 찾아볼 수 있다. 잘 모르겠다면 0.01 정도로 한 번 밀어보고 결과에 따라 조정하는 것도 방법이다. 학습률이 큰지/ 작은지는 Training 중 Loss를 보면 알 수 있다. 이것까지 다루기에는 글이 길어지니 넘어가겠다.

경사하강법으로 계산해 보기

이제 구체적으로 계산 방법에 대해 이야기할 차례다. 편미분에 대해서는 미리 알고 있어야 계산 과정을 이해할 수 있다.

$f(x)=w_1x+w_0$이라는 일차 함수가 있다. 일차 함수를 완성하기 위해 우리는 $W {w_1, w_0}$를 업데이트한다.

앞에서 정의했듯이 모델을 거쳐 나온 예측 값(출력값)은 $f(x)$이다. 그리고 실제 값은 $y$라고 하겠다. 모델의 오차란 예측 값과 실제 값 사이의 차이를 뜻한다. 기호로 표현하면 $f(x)-y$이다. 우리는 오차의 크기가 궁금하지 부호는 관심 없기 때문에 제곱을 통해 부호를 없애주겠다. 

$E(x)=(f(x)-y)^2$

이제 오차 값을 구하는 $E(x)$가 대충 정의되었다. 그런데 실제 학습에서는 데이터를 하나만 사용할 수 없다. 1차 함수가 (0, -1)를 지난다는 데이터 하나만 가지고는 $2x-1$인지 $1234x-1$인지 특정할 수 없다. 따라서 모든 X, Y에  대해 오차를 구해서 평균을 낸다.

$E(x)=\cfrac{1}{N}\sum_i^N (f(x_i)-y_i)^2$

이제야 비용 함수가 완전히 정의되었다. 참고로 이렇게 빼고 제곱해서 오차를 구하는 방식을 MSE (Mean Square Loss)라고 한다.

위 내용이 정리되었다면 $f(x)$에 원래 식을 대입해 보자.

$E(x)=\cfrac{1}{N}\sum_i^N (w_1x_i+w_0-y_i)^2$

식이 복잡해 보여도 과정만 이해했다면 전혀 걱정할 필요 없다. 어차피 계산은 컴퓨터가 할 거다.

이제 비용 함수 $E(x)$에 가중치 값인 $W$가 포함되어 있는 것을 볼 수 있다. 우리의 목적은 W값을 업데이트하는 것이기 때문에 $W$를 중심으로 정의한 $E(W)$를 목적 함수로 둔다. 식이 달라진 것은 없다.

\[E(W)=\cfrac{1}{N}\sum_i^N (w_1x_i+w_0-y_i)^2\]

이제 경사 하강법으로 계산할 준비가 끝났다. 

\[w^{t+1}=w^t-\mu\cfrac{dE(W)}{dw}\]

위에서 봤던 경사 하강법 식이다. 우리는 $w_1$과 $w_0$라는 2개의 가중치가 있기 때문에 각각에 대해 편미분을 수행하고 업데이트해주어야 한다. $E(W)$ 자리에 목적 함수를 대입하고 편미분을 수행한다. 어차피 $\mu$라는 상수가 곱해져 있기 때문에 간단하게 다른 상수 값은 생략하고 계산하겠다. 

$w_1\rightarrow w_1-\mu\cfrac{dE(W)}{dw_1} \ =w_1-\mu\cfrac{1}{N}\sum_i^N 2(w_1x_i+w_0-y_i)x_i \ =w_1-\mu\sum_i^N(w_1x_i+w_0-y_i)x_i$

$w_0\rightarrow w_0-\mu\cfrac{dE(W)}{dw_0} \ =w_0-\mu\cfrac{1}{N}\sum_i^N2(w_1x_i+w_0-y_i) \ =w_0-\mu\sum_i^N(w_1x_i+w_0-y_i)$

이렇게 $w_1, w_0$값을 업데이트하는 과정을 계속 반복하면 최적의 값을 찾을 수 있다. 

이쯤 되면 ‘이거 더 쉽게 풀 수 있을 거 같은데’하는 생각이 들 수 있다. 아래에서 보여줄 예시는 연립 방정식으로 푸는 게 더 쉽고 빠르다. 하지만 실생활에서 발생하는 문제들은 훨씬 복잡하다. 예를 들어, 쓰레기 이미지 1000장을 가지고 ‘종이와 플라스틱을 분류하는 모델을 만들고 학습해라’라고 한다면 머리가 하얘질 거다. 이런 상황에서도 오차를 최소화할 수 있도록 일반화한 것이 경사하강법이라고 보면 된다. 

Python으로 테스트

아래 예제는 Linear Regression이라는 문제를 경사하강법을 활용해 해결하는 과정이다. 

$X={0, 1, 3}$

$Y={-1, 1, 5}$

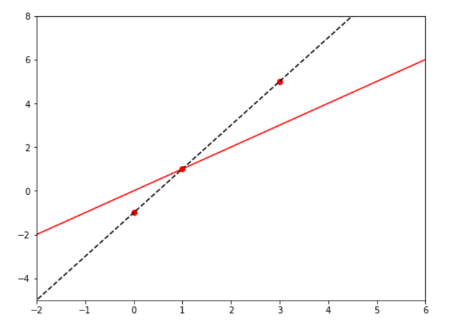
우리는 빨간 직선과 같이 임의의 일차 함수를 만들고 경사 하강법을 이용해 데이터 간 오차를 줄여나갈 것이다. 최종적으로 검정 점선과 같이 데이터에 대해 오차가 작아지도록 만드는 것이 목표이다. 

$f(x)=w_1x+w_0=1x+0$

직선을 만들고 가중치를 $w_1=1$, $w_0=0$으로 랜덤하게 정했다. 이 함수에서 업데이트해야 하는 가중치는 $w_1, w_0$이다.

그리고 위에서 열심히 풀었던 과정을 코드로 옮겨보았다. 손으로 계산하면 오래 걸리지만 컴퓨터로 계산하면 0.01초 정도 걸린다. Python을 잘 모른다면 그냥 #으로 적힌 부분을 따라가면서 어떤 과정으로 코드가 실행되었는지만 봐도 충분하다. 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40

# 사용할 데이터: X, Y
X_ = [0, 1, 3]
Y_ = [-1, 1, 5]

# 데이터의 크기: n
n = len(X_)

# 가중치 초기화: f(x) = 1x + 0
w_ = [0, 1]  # [w0, w1]

# 함수 정의: f(x) = w1 * x + w0
def f(x):
    pred = w_[1] * x + w_[0]
    return pred

# 비용 함수: E(x) = 1/N * Sum(f(xi) - yi)^2
def cost():
    error = 1 / n * sum((f(X_[i]) - Y_[i])**2 for i in range(n))
    return error

# 학습률
lr = 0.1

# 업데이트를 몇 번 반복할지 결정
n_iter = 20

for iter in range(1, n_iter+1):
    # 경사하강법으로 반복
    print(f"[{iter}번째 업데이트]")

    # 가중치 업데이트
    w_[1] = w_[1] - lr * sum((f(X_[i]) - Y_[i]) * X_[i] for i in range(n))
    w_[0] = w_[0] - lr * sum([(f(X_[i]) - Y_[i]) for i in range(n)])

    # 업데이트된 가중치 보기
    print(f" f(x) = {w_[1]:.2f}x {w_[0]:.2f}")

    # 오차 확인하기 
    error = cost()
    print(f" 오차: {error:.5f}\n")

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

[1번째 업데이트]
 f(x) = 1.60x -0.14
 오차: 0.35560

[2번째 업데이트]
 f(x) = 1.66x -0.26
 오차: 0.26300

[3번째 업데이트]
 f(x) = 1.70x -0.36
 오차: 0.19452
 
 ...

[20번째 업데이트]
 f(x) = 1.98x -0.95
 오차: 0.00115

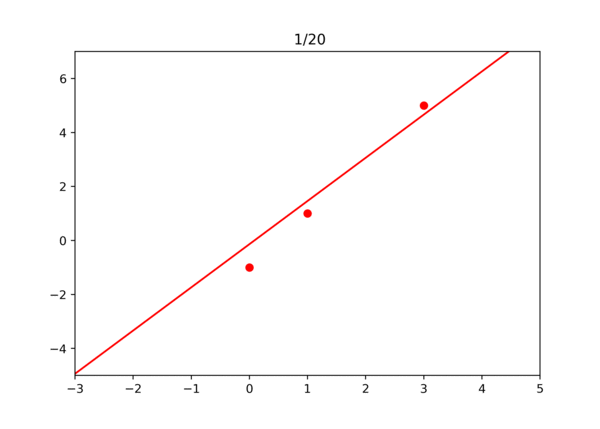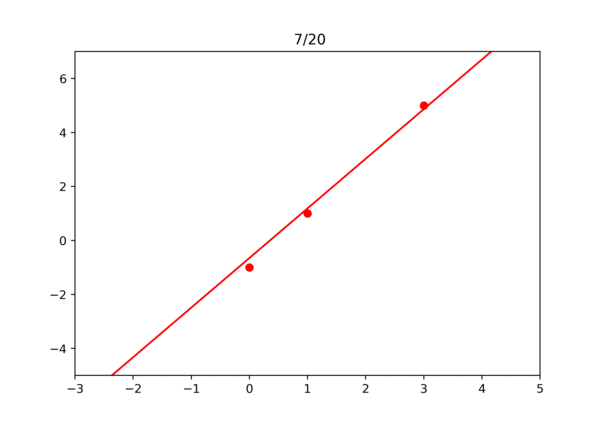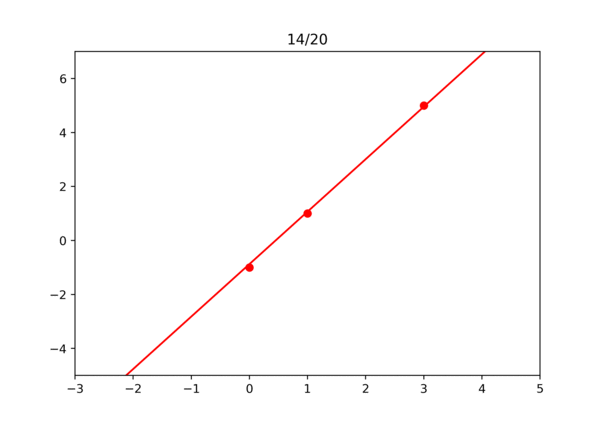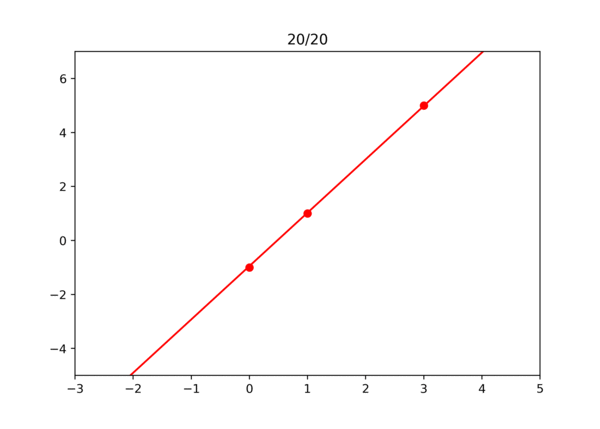
값이 점점 업데이트되면서 오차가 감소하는 것을 볼 수 있다. 20번 정도 반복하고 확인해보니 오차가 아주 작아졌다. 30번 반복하면 오차가 0.00006까지 감소한다. 

학습되는 과정을 영상으로 확인하면 아래와 같다. 

이걸로 경사 하강법이 잘 작동한다는 것을 확인해 보았다. 물론 실제로는 손으로 하나하나 미분하지 않고 자동으로 계산한다. 역방향으로 미분값 계산 참고.

마지막으로 테스트해볼 것은 학습률이다. 학습률이 커지면 값이 튄다고 했는데 어떤 의미인지 직접 확인해 보겠다. 위 예시는 학습률을 0.1로 두고 학습했다. 이번에는 같은 문제를 학습률 0.5로 학습해 보았다. 학습률을 제외하고 다른 요소는 모두 동일하다. 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

[1번째 업데이트]
 오차: 9.58333

[2번째 업데이트]
 오차: 4.06250

[3번째 업데이트]
 오차: 39.76562
  
  ...
  
[29번째 업데이트]
 오차: 537407805.94885

[30번째 업데이트]
 오차: 5223270089.75743

값을 보면 자기 멋대로 커졌다 작아졌다를 반복한다. 결국 30번 정도 돌렸을 때 오차가 처음보다 더 커졌다. 이럴 거면 차라리 눈 가리고 아무 값이나 찍는 게 더 정확하다. 그렇기 때문에 오차 값을 보고 뭔가 이상하다 싶으면 학습률을 줄여가며 ‘적당한’ 학습률을 찾아야 한다.

Pytorch

Pytorch는 미분값을 자동으로 계산한다. torch를 잘 모른다면 #으로된 주석만 봐도 괜찮다.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

import torch

# 학습할 X, y를 tensor로 정의
x_train = torch.as_tensor(x_train)
y_train = torch.as_tensor(y_train)
# 학습률
lr = 0.2

# 가중치를 랜덤하게 초기화
w_1 = torch.rand(1, requires_grad=True)
w_0 = torch.rand(1, requires_grad=True)

for iter in range(1, 31):
    # 예측값
    pred = w_1 * x_train + w_0
    # 손실 함수
    loss = ((pred - y_train)**2).mean()

    # 가중치의 미분값 기억하기
    w_1.retain_grad()
    w_0.retain_grad()

    # 역방향으로 미분값 계산
    loss.backward()
    # 가중치 업데이트
    w_1 = w_1 - lr * w_1.grad
    w_0 = w_0 - lr * w_0.grad

    if iter % 5 == 0:
        print(f"[{iter}번째 업데이트]")
        print(f" - 오차: {loss.item():.5f}\n")
    
print(f"w_1: {w_1.item():.3f}, w_0: {w_0.item():.3f}")
AI
Python AI
이 글은 저작권자의 CC BY-NC 4.0 라이센스를 따릅니다.

인기 태그

AI Python CV Go Pytorch blog NLP