SVD를 이용한 이미지 압축

게시 2025/01/08

By 박성진

SVD: Singular Vector Decomposition에 대해 다룬다. 각 수식이 어떤 의미를 가지고, 이미지 압축에 어떻게 사용되는지 설명한다. 본 글을 이해하기 위해 아래 개념을 숙지하고 있어야 한다.

Vector: 크기와 방향을 가지는 양으로, 2차원 공간의 벡터는 $\vec{v}=\begin{bmatrix}u_1 & u_2\end{bmatrix}$와 같이 표현한다. 본문에서는 편의상 $v$ 형태로 표기한다.

Inversed matrix: $A$에 대한 역행렬로 $A^{-1}$로 표기하며, $A^{-1}A=I$라는 특징을 가진다.

Orthogonal matrix: 모든 column 벡터가 직교하는 행렬로, $AA^T=A^TA=I$라는 특징을 가진다. 동시에 $A^T=A^{-1}$이다.

Diagonal matrix: 주대각 성분을 제외한 모든 값이 0이며, $diag(u_1,u_2 …)$로 표현한다.

선형 변환: $s\cdot \vec{v}$를 통해 벡터의 크기와 방향을 왜곡할 수 있다.

Eigenvector의 특징

eigenvector는 고윳값으로 불리며, 선형 변환이 발생해도 방향을 유지하는 벡터를 말한다. eigenvector를 검색하면 다음과 같은 식이 나온다.

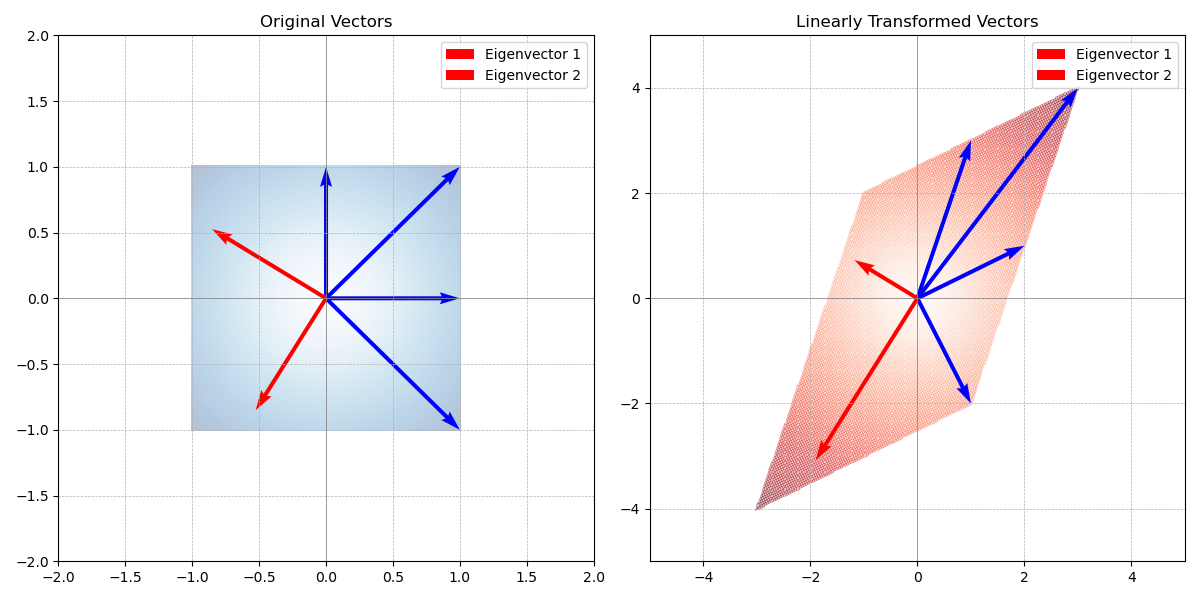
\[Av=\lambda v\]

식만 봐서는 모르겠으니, 한 단계씩 해석해 보자. $Av$는 벡터 $v$에 행렬 $A$를 곱해 선형 변환을 했다. 이 과정에서 대부분의 벡터는 왜곡된다.

\[Av=\begin{bmatrix}2 & 1 \\ 1 & 3 \end{bmatrix}v\]

하지만 같은 방향을 유지하는 벡터도 존재한다. 이 벡터를 eigenvector라고 부른다. 방향은 유지하고 있지만 크기는 바뀌었다. 따라서 변형된 벡터를 $\lambda v$로 표현할 수 있다. $\lambda$는 크기를 조절하는 scaling factor 역할을 한다. eigenvector의 크기를 결정하는 $\lambda$를 eigenvalue라고 한다.

        
      
>>> eigenvalues, eigenvectors = np.linalg.eig(transformation_matrix)
>>> eigenvectors
[[-0.85065081 -0.52573111]
 [ 0.52573111 -0.85065081]] 
>>> eigenvalues
[1.38196601 3.61803399]

다시 처음으로 돌아와 $Av=\lambda v$는 벡터 $v$에 $A$를 통해 선형 변환을 해도 여전히 $v$인 (0이 아닌) 벡터를 eigenvector라고 한다. 이때 eigenvector에 곱해진 scaling factor를 eigenvalue라고 한다.

eigen-decomposition

eigenvector와 eigenvalue를 알면, 변환 행렬 $A$를 찾을 수 있다.

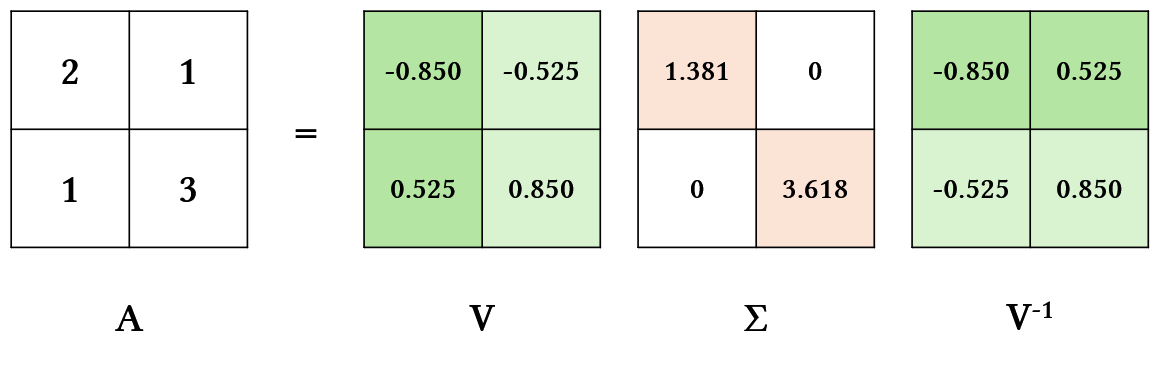
\[A=V\Sigma V^{-1}\]

$V$는 각 열이 eigenvector인 행렬이다. $\Sigma =diag(…eigenvalue)$로 eigenvalue를 담고 있는 diagonal matrix이다.

다시 말해, 행렬 A는 eigenvector와 eigenvalue로 분해(decompose)할 수 있고, 이 값들을 통해 재구성할 수 있다. 이 개념이 이미지를 압축하고 재구성하는 과정에도 적용된다. 하지만 eigendecomposition은 n x n의 square matrix에만 적용 가능하다. 따라서 eigenvector 대신 singular vector가 등장한다.

SVD

orthogonal matrix $U$와 $V$에 대해 아래 식이 성립한다.

\[A=U\Sigma V^T\]

$A$는 m x n 크기의 행렬이며, $\Sigma$는 diagonal matrix이다. 식을 정리해 보면 다음과 같다.

\[AV=U\Sigma\]

이번에는 orthogonal matrix $V$와 선형 변환해도 여전히 orthogonal 한 $U$를 찾는 문제다.

식을 조금 더 정리해보면,

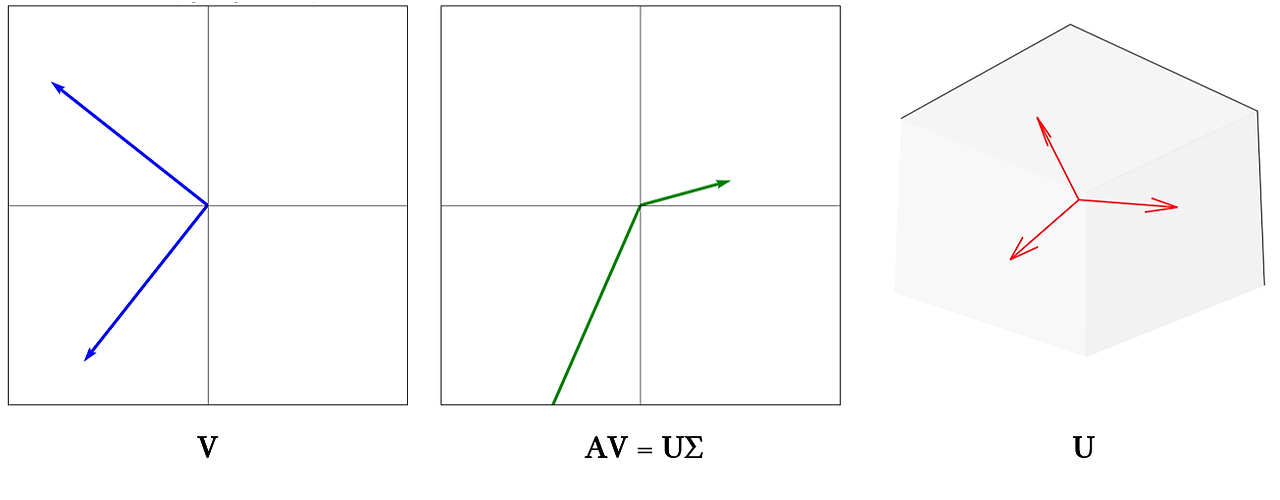
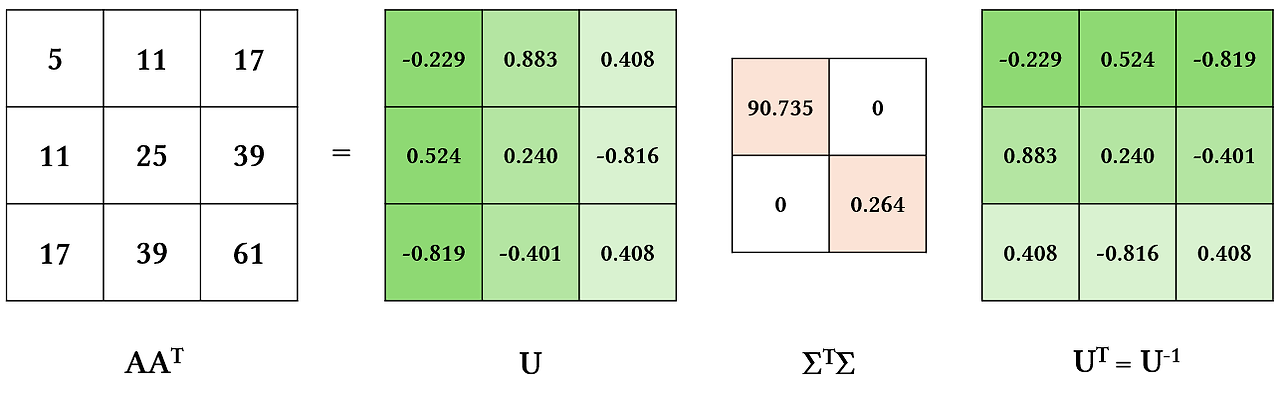
\[AA^T=U\Sigma V^T (V\Sigma^T U^T)\] \[AA^T=U(\Sigma^T\Sigma)U^T\]

글 초반에 소개했던 행렬의 특성을 이용해 정리한 식이다. 위 식을 시각화하면 다음과 같다.

눈치챘다시피 $U$는 eigenvector와 동일하다. $\Sigma^T\Sigma$는 diagonal matrix로 eigenvalue와 같다.

식을 $V$에 대해 정리하면,

\[A^TA=V(\Sigma^T\Sigma)V^T\]

따라서 $V$도 eigenvector와 같은 성질을 가진다.

용어 정리

$U$와 $V$는 singular vector로 eigenvector와 같은 의미를 가진다. $\Sigma$는 singular value로 eigenvalue와 동일하다.

\[A=U\Sigma V^T\]

$U$: Left Singular Vector
$V$: Right Singular Vector
$\Sigma$: Singular Value

정리하면, $A$는 singular vector $U$와 $V$로 분해되며, $\Sigma$는 scaling 정도를 나타내는 singular value이다.

        
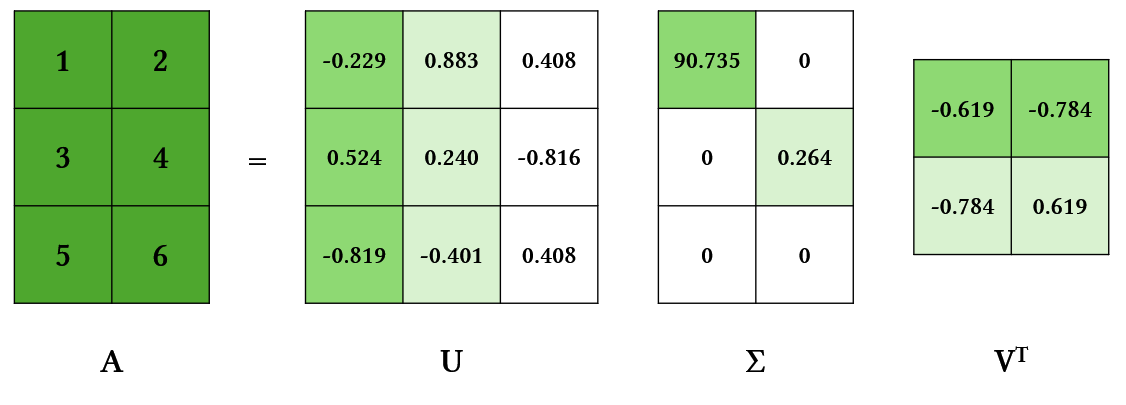
A = np.array([[1, 2], [3, 4], [5, 6]])

# Perform SVD (A = U * Σ * V^T)
U, sigma, Vt = np.linalg.svd(A)

Truncated SVD

서로 다른 자연수 m과 n에 대해, m x n 행렬에 SVD를 수행하면 버려지는 singular vector가 존재한다. 3 x 2 행렬을 살펴보자.

left singular vector인 $U$는 색칠된 3 x 2 행렬의 값만 연산에 사용한다. 따라서 3 x 3이 아닌 3 x 2 행렬만 저장하면 된다. singular value인 $\Sigma$ 도 [0 0]을 저장하고 있는 행은 버려도 된다.

따라서 m > n일 때는 left singular vector가 m x n이 되고, m < n일 때는 right singular vector가 m x n이 된다. singular value는 min(m, n) 크기의 square matrix가 된다.

이미지 분해

이미지 가로 길이가 $w$, 세로 길이가 $h$일 때, 2차원 이미지는 $h\times w$ 행렬로 표현할 수 있다. 이미지 행렬을 $M$라고 할 때, 다음과 같이 분해할 수 있다.

\[M=U\Sigma V^T\] \[U=[u_1, u_2 ... u_h]\] \[V=[v_1, v_2 ... v_w]\] \[\Sigma=diag(\sigma_1, \sigma_2, ... \sigma_n)\]

SVD에 재밌는 특징이 있는데 singular value가 큰 값부터 내림차순으로 나열되어 있다는 점이다. $\sigma$ 중 $\sigma_1$이 가장 큰 값을 갖는다. 즉, 첫 번째 값부터 순서대로 중요한 정보를 담고 있다.

“중요한” 정보란 variance를 크게 높이는 값을 말한다. variance는 데이터가 얼마나 넓게 또는 복잡하게 퍼져있는가를 나타낸다. eigenvalue와 singular value는 scaling factor로 벡터를 얼마나 크게 늘릴지 결정하는 요소다. 그렇기 때문에 큰 value는 vector를 넓게 퍼질 수 있도록 하고, 데이터 variance도 증가시킨다. 따라서 singular value가 큰 vector는 더 중요한 정보를 담고 있다고 표현할 수 있다. 자세한 내용은 아래 PCA에서 다룬다.

이미지 행렬 $M$은 $\sum_{n=1} \sigma_n u_n v_n^T$으로 표현할 수 있다. 그런데 만약 정보를 전부 사용하지 않고, 중요한 정보 몇 가지만 사용하면 어떨까?

가로 500, 세로 600의 600 x 500 행렬에 대해 실험을 해보았다.

당연히 벡터를 많이 사용할수록 이미지가 선명해진다.

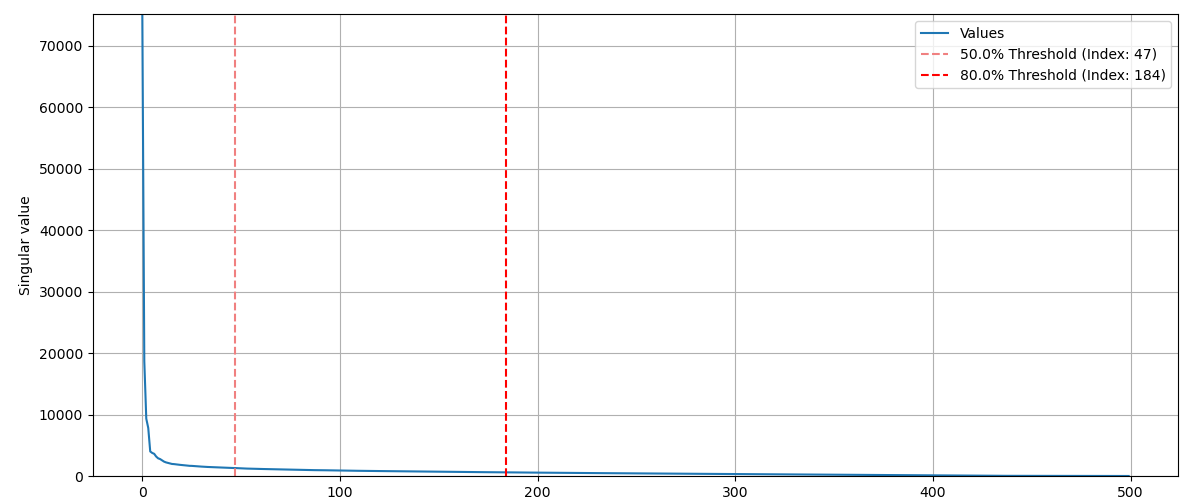
singular value를 시각화해보면 n = 184에서 이미 singular value 총합의 80%를 넘어간다. 184 쌍의 singular vector만으로도 이미지 80%를 복원할 수 있다.

만약 600 x 500 행렬을 모두 사용하면 총 300,000개의 정보가 필요하다. 하지만, n = 200이라면 총 220,200개의 정보만 있으면 된다.

SVD는 np.linalg.svd를 통해 계산한다. full_matrices 옵션은 불필요한 벡터를 저장할지 결정한다.

        
      
"""이미지 분해 및 재구성"""

import numpy as np
from PIL import Image
import os

image_path = "object4.jpg"
output_dir = "svd_images"

image = Image.open(image_path).convert("L")
image = np.array(image, dtype=np.float64)

# Singular Vector Decomposition (SVD)
# Image: (600, 500), S: (500,), Vt: (500, 500)
# U: (600, 500) when full_matrices=False
# U: (600, 600) when full_matrices=True
U, S, Vt = np.linalg.svd(image, full_matrices=False)

# 이미지 재구성
for n in range(1, len(S) + 1):
    singular_values = np.zeros((U.shape[1], Vt.shape[0]))
    np.fill_diagonal(singular_values, S[:n])
    reconstructed = np.dot(
        U[:, :n],
        np.dot(singular_values[:n, :n], Vt[:n, :]),
    )
    output_image = np.clip(reconstructed, 0, 255).astype(np.uint8)

    # 단계별 이미지 저장
    if n % 10 == 0:
        output_path = os.path.join(output_dir, f"{n}.png")
        Image.fromarray(output_image).save(output_path)

        
      
"""Singular value 시각화"""

from PIL import Image
import numpy as np
import matplotlib.pyplot as plt

image = Image.open("object4.jpg").convert("L")
image = np.array(image, dtype=np.float64)

U, S, Vt = np.linalg.svd(image, full_matrices=False)

cumulative_sum = np.cumsum(S)
total_sum = np.sum(S)
threshold_percentage_1 = 0.5
threshold_percentage_2 = 0.8
threshold_1 = total_sum * threshold_percentage_1
threshold_2 = total_sum * threshold_percentage_2

threshold_index_1 = np.argmax(cumulative_sum >= threshold_1)
threshold_index_2 = np.argmax(cumulative_sum >= threshold_2)

plt.figure(figsize=(14, 6))
plt.plot(range(len(S)), S, label="Values")
plt.axvline(
    x=threshold_index_1,
    color="lightcoral",
    linestyle="--",
    label=f"{threshold_percentage_1 * 100}% Threshold (Index: {threshold_index_1})",
)
plt.axvline(
    x=threshold_index_2,
    color="red",
    linestyle="--",
    label=f"{threshold_percentage_2 * 100}% Threshold (Index: {threshold_index_2})",
)

plt.xlabel("Index")
plt.ylabel("Singular value")
plt.ylim(0, S[0] + 1)
plt.legend()
plt.grid(True)
plt.show()

PCA: 주성분 분석

PCA: Principle Component Analysis는 데이터의 주요한 특징을 찾아 차원을 축소하는 기법이다. 정확히 공분산 행렬에 대해 eigen-decompotion 또는 SVD를 수행한다. 본 글은 SVD를 기준으로 설명하며, scikit-learn도 SVD를 기반으로 구현되어 있다.

공분산(covariance)은 고차원 행렬에 대한 분산이다. $n\times d$ 크기의 데이터 행렬을 $X$, 데이터 평균을 $\mu$라고 할 때, 공분산 행렬 $\Sigma$는 다음과 같다.

\[\Sigma=\cfrac{1}{n-1}(X-\mu)^T(X-\mu)\]

공분산 행렬을 구하기 전 원점을 중심으로 $X$를 이동시킨다. 그리고 공분산 행렬에 대해 SVD를 실행한다.

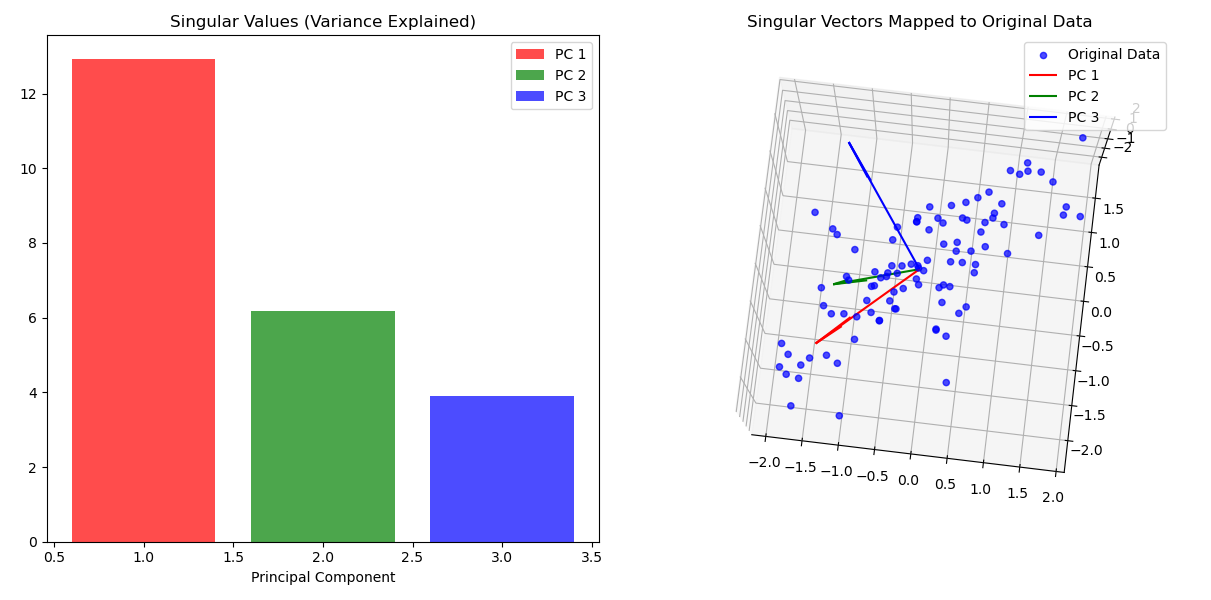
공분산 행렬에 대한 Singular vector를 시각화한 그래프다. 데이터의 중심축을 따라 vector가 만들어진 것을 확인할 수 있다. Singular vector가 만드는 축을 Principle Component라고 부른다. 그림에서 빨간 색으로 표현된 Component 1이 가장 큰 singular value를 가진다. 동시에 데이터 정보를 가장 잘 표현한 축이다. 따라서 3차원 데이터를 Component 1에 대해 매핑하면 차원 축소가 일어난다.

데이터의 주요한 분포를 유지한 채 차원만 축소시켰다.

        
      
import numpy as np
from sklearn.decomposition import PCA

data = # load dataset
pca = PCA(n_components=1)
pca.fit(data)

singular_vectors = pca.components_
singular_values = pca.singular_values_
cov_matrix = np.cov(data.T)

참고자료

Machine-Learning

Python CV AI